题目内容
15.已知数列{an}中,${a_1}=1,{a_{n+1}}=\frac{a_n}{{{a_n}+1}}$如果${b_n}=\frac{a_n}{n+2}$,则数列{bn}的前n项和为$\frac{3}{4}$-$\frac{2n+3}{2({n}^{2}+3n+2)}$.分析 由${a_1}=1,{a_{n+1}}=\frac{a_n}{{{a_n}+1}}$,两边取倒数可得:$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=1,利用等差数列的通项公式可得:an=$\frac{1}{n}$.可得bn=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,再利用“裂项求和”即可得出.
解答 解:∵${a_1}=1,{a_{n+1}}=\frac{a_n}{{{a_n}+1}}$,
两边取倒数可得:$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=1,
∴数列$\{\frac{1}{{a}_{n}}\}$是等差数列,首项为1,公差为1,
∴$\frac{1}{{a}_{n}}$=1+(n-1)=n,
∴an=$\frac{1}{n}$.
∴${b_n}=\frac{a_n}{n+2}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
则数列{bn}的前n项和=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})+(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$
=$\frac{3}{4}$-$\frac{2n+3}{2({n}^{2}+3n+2)}$.
点评 本题考查了“裂项求和”方法、等差数列的通项公式、递推式的应用,考查了变形能力、推理能力与计算能力,属于中档题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 既非充分又非必要条件 |
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| A. | 函数f(x)在[a,b]上不一定有最小值 | |
| B. | 函数f(x)在[a,b]上有最小值,但不一定是f(x0) | |
| C. | 函数f(x)在[a,b]上有最小值f(x0) | |
| D. | 函数f(x)在[a,b]上的最大值也可能是f(x0) |
| A. | 60° | B. | 60°或120° | C. | 30° | D. | 30°或150° |
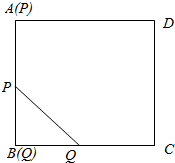 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |