题目内容
3.定义在闭区间[a,b]上的连续函数y=f(x)有唯一的极值点x=x0,且y极小值=f(x0),则下列说法正确的是( )| A. | 函数f(x)在[a,b]上不一定有最小值 | |
| B. | 函数f(x)在[a,b]上有最小值,但不一定是f(x0) | |
| C. | 函数f(x)在[a,b]上有最小值f(x0) | |
| D. | 函数f(x)在[a,b]上的最大值也可能是f(x0) |
分析 先求出函数的单调区间,从而求出函数的极小值也是函数的最小值,从而求出答案.
解答 解:∵连续函数y=f(x)在[a,b]上有唯一的极值点x=x0,且y极小值=f(x0),
∴函数y=f(x)在[a,x0)递减,在(x0,b]递增,
∴y最小值=y极小值=f(x0),
故选:C.
点评 本题考察了函数的单调区间,考察函数的极值问题,考察导数的应用,本题属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.抛物线y=$\frac{1}{4}$x2的准线方程是( )
| A. | $x=-\frac{1}{16}$ | B. | $x=-\frac{1}{8}$ | C. | y=-1 | D. | y=-2 |
11.若函数f(x)=x3-mx2-x+5在区间(0,1)内单调递减,则实数m的取值范围是( )
| A. | m≥1 | B. | m=1 | C. | m≤1 | D. | 0<m<1 |
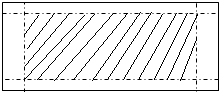 为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小?
为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小?