题目内容
10.在△ABC中,已知a=40,b=20$\sqrt{2}$,A=45°,则角B等于( )| A. | 60° | B. | 60°或120° | C. | 30° | D. | 30°或150° |
分析 由正弦定理可得sinB=$\frac{bsinA}{a}$=$\frac{1}{2}$,由于a=40>b=20$\sqrt{2}$,可得范围0<B<45°,从而可求B的值.
解答 解:由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{20\sqrt{2}×sin45°}{40}$=$\frac{1}{2}$.
由于a=40>b=20$\sqrt{2}$,可得0<B<45°,
可得:B=30°,
故选:C.
点评 本题主要考查了正弦定理,大边对大角等知识的应用,属于基本知识的考查.

练习册系列答案
相关题目
5.函数f(x)=x3+bx2+cx+d的图象如图所示,则函数g(x)=log2(x2+$\frac{2b}{3}$+$\frac{c}{3}$)的单调递减区间是( )
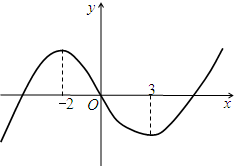

| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
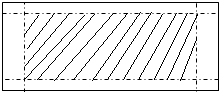 为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小?
为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小?