题目内容
【题目】已知点Pn(an ， bn)满足an＋1＝an·bn＋1 ， bn＋1＝(n∈N*)且点P1的坐标为(1，－1)．
（1）求过点P1 ， P2的直线l的方程；
（2）试用数学归纳法证明：对于n∈N* ， 点Pn都在(1)中的直线l上．
【答案】
（1）
【解答】
由P1的坐标为（1，-1）知a1=1,b1=-1.
所以
所以点p2的坐标为
所以直线l的方程为2x+y=1.
（2）
【解答】
证明：（1）当n=1时，2a1+b1=2
1+(-1)=1成立。
（2）假设n=k
时，2ak+bk=1成立。
则当n=k+1时，
所以当n=k+1时，命题也成立。
由（1）（2）知，对
,都有2an+bn=1,
即点Pn在直线l上.
【解析】一般地，证明一个与正整数n有关的命题，可按下列步骤进行：(1)(归纳奠基)证明当n取第一个值时命题成立；(2)(归纳递推)假设n＝k(k≥n0，k∈N+)时命题成立，证明当n=k+1时命题也成立．
只要完成这两个步骤，就可以断定命题对从n0开始的所有正整数n都成立．上述证明方法叫做数学归纳法
【考点精析】解答此题的关键在于理解数学归纳法的步骤的相关知识，掌握
- 步骤:A.命题在n=1（或
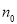）时成立，这是递推的基础；B.假设在n=k时命题成立； C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=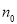,且
)结论都成立
．
练习册系列答案
相关题目
