题目内容
【题目】已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.
(1)判断直线l与圆C的位置关系;
(2)若定点P(1,1)分弦AB为 ![]() =
= ![]() ,求此时直线l的方程.
,求此时直线l的方程.
【答案】
(1)解:由于直线l的方程是mx﹣y+1﹣m=0,即 y﹣1=m(x﹣1),经过定点H(1,1),
而点H到圆心C(0,1)的距离为1,小于半径 ![]() ,故点H在圆的内部,故直线l与圆C相交,
,故点H在圆的内部,故直线l与圆C相交,
故直线和圆恒有两个交点
(2)解:设A(x1,y1),B(x2,y2),由 ![]() =
= ![]() ,得
,得 ![]() =
= ![]()
![]() ,
,
∴1﹣x1= ![]() (x2﹣1),化简的x2=3﹣2x1…①
(x2﹣1),化简的x2=3﹣2x1…①
又由直线代入圆的方程,消去y得:(1+m2)x2﹣2m2x+m2﹣5=0…(*)
∴x1+x2= ![]() …②
…②
由①②解得x1= ![]() 代入(*)式解得m=±1,
代入(*)式解得m=±1,
∴直线l的方程为x﹣y=0或x+y﹣2=0
【解析】(1)根据直线l的方程可得直线经过定点H(1,1),而点H到圆心C(0,1)的距离为1,小于半径,故点H在圆的内部,故直线l与圆C相交,命题得证.(2)把线段的长度比转化为两个向量的关系,由向量的坐标运算得到A,B两点横坐标间的关系,联立直线与圆的方程化为关于x的一元二次方程,由根与系数关系得到A,B两点横坐标的和,求出其中一点的横坐标,最后再代入关于x的方程得到关于m的方程,求解得到m的值,则直线方程可求.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案【题目】利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
月份 | 2 | 3 | 4 | 5 |
产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图; 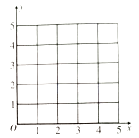
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量? (注:回归方程 ![]() =
= ![]() x+
x+ ![]() 中,
中, ![]() =
= 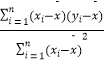 =
= 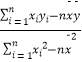 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)