题目内容
【题目】设f(x)是二次函数，其图象过点(0,1)，且在点(－2，f(－2))处的切线方程为2x＋y＋3＝0
（1）求f(x)的表达式；
（2）求f(x)的图象与两坐标轴所围成图形的面积；
（3）若直线x＝－t(0<t<1)把f(x)的图象与两坐标轴所围成图形的面积二等分，求t的值．
【答案】
（1）
【解答】设f(x)＝ax2＋bx＋c，
∵其图象过点(0,1)，∴c＝1，
又∵在点(－2，f(－2))处的切线方程为2x＋y＋3＝0，∴ 
∵f′(x)＝2ax＋b，∴ 
∴a＝1，b＝2，故f(x)＝x2＋2x＋1．
（2）
【解答】依题意，f(x)的图象与两坐标轴所围成的图形如图中阴影部分所示，
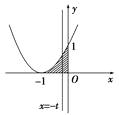
故所求面积 
（3）
【解答】依题意，有
即
所以
所以
所以
【解析】中档题，考查定积分在求解面积中的运用。理解并掌握定积分与面积的关系，函数f(x)与x=a,x=b,y=0所围成的封闭图形的面积为
练习册系列答案
阅读快车系列答案
相关题目
