题目内容
20．
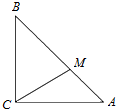如图，在△ABC中，∠ACB=90°，且AC=BC=3，点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$，（1）用$\overrightarrow{CA}$、$\overrightarrow{CB}$向量表示向量$\overrightarrow{CM}$．
（2）求|$\overrightarrow{CM}$|．
分析 （1）根据题意建立平面直角坐标系，求出M的坐标，然后根据平面向量的基本定理，设$\overrightarrow{CM}={λ}_{1}\overrightarrow{CA}+{λ}_{2}\overrightarrow{CB}$，可求出${λ_1}=\frac{2}{3}，{λ_2}=\frac{1}{3}$
（2）利用坐标求模长．
解答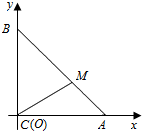 
解：如图建立平面直角坐标系．由题意知：A（3，0），B（0，3），…（1分）
设M（x，y），由$\overrightarrow{BM}=2\overrightarrow{MA}$得：（x，y-3）=2（3-x，-y），
∴$\left\{\begin{array}{l}{x=2（3-x）}\\{y-3=-2y}\end{array}\right.$，∴$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$，∴M（2，1）…（4分）
（1）设$\overrightarrow{CM}={λ}_{1}\overrightarrow{CA}+{λ}_{2}\overrightarrow{CB}$，可求出${λ_1}=\frac{2}{3}，{λ_2}=\frac{1}{3}$，∴$\overrightarrow{CM}=\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$…（8分）
（2）∵$\overrightarrow{CM}=（2，1）$，∴$|{\overrightarrow{CM}}|=\sqrt{{2^2}+{1^2}}=\sqrt{5}$．…（12分）
点评 本题考查了平面向量的基本定理及坐标表示模长，属于中档题．
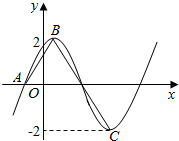已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点．若f（0）=$\sqrt{3}$，且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8．则f（x）的解析式为（ ）
| A． | f（x）=2sin（2x+$\frac{π}{3}$） | B． | f（x）=2sin（2x+$\frac{π}{6}$） | C． | f（x）=2sin（3x+$\frac{π}{3}$） | D． | f（x）=2sin（3x+$\frac{π}{6}$） |