题目内容
10.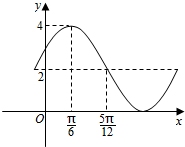 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
分析 先根据函数的最大值和最小值求得A和B,然后利用图象中$\frac{5π}{12}$-$\frac{π}{6}$求得函数的周期,求得ω,最后根据x=$\frac{π}{6}$时取最大值,求得φ,即可得解.
解答 解:如图根据函数的最大值和最小值得|A|+B=4,|A|-B=0,、
∵A>0,
∴A=2,B=2,
函数的周期为($\frac{5π}{12}$-$\frac{π}{6}$)×4=π,
又∵ω>0,
∴ω=2,
当x=$\frac{π}{6}$时取最大值,即sin(2×$\frac{π}{6}$+φ)=1,2×$\frac{π}{6}$+φ=2kπ+$\frac{π}{2}$,k∈Z,
∴φ=2kπ-$\frac{π}{6}$,k∈Z,
∵|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
∴解析式为:y=2sin(2x+$\frac{π}{6}$)+2.
故答案为:y=2sin(2x+$\frac{π}{6}$)+2.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了学生基础知识的运用和图象观察能力,属于基本知识的考查.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
18.若$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-4,7),则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{65}}}{5}$ | C. | 13 | D. | $\sqrt{65}$ |
5.某小区有老年人28个,中年人57个,年轻人63个,为了调查他们的身体健康状况,从他们中抽取容量为21的样本,最适合抽取样本的方法是( )
| A. | 简单随机抽样 | |
| B. | 系统抽样 | |
| C. | 分层抽样 | |
| D. | 先从中年人中随机剔除1人,再用分层抽样 |
15.下列给出的赋值语句正确的是( )
| A. | 6=A | B. | M=-M | C. | B=A=2 | D. | x+5y=0 |
19.不等式|3x-4|≤5的解集是( )
| A. | {x|-$\frac{1}{3}$<x<3} | B. | {x|x≤-$\frac{1}{3}$或x≥3} | C. | {x|$\frac{1}{3}$≤x≤-3} | D. | {x|-$\frac{1}{3}$≤x≤3} |
20.设等差数列{an}的前n项和为Sn,若$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{3}$,则$\frac{S_6}{{{S_{12}}}}$的值为( )
| A. | $\frac{10}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |