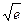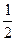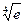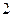题目内容
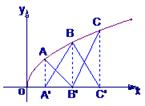
如图,点A、B、C都在函数y=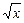 的图像上,它们的横坐标分别是a、a+1、a+2
的图像上,它们的横坐标分别是a、a+1、a+2 又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
(1)求函数f(a)和g(a)的表达式;
(2)比较f(a)与g(a)的大小,并证明你的结论.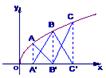
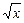 的图像上,它们的横坐标分别是a、a+1、a+2
的图像上,它们的横坐标分别是a、a+1、a+2 又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a). (1)求函数f(a)和g(a)的表达式;
(2)比较f(a)与g(a)的大小,并证明你的结论.

(1) f(a) =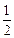 (
( ),g(a)=
),g(a)= (2) f(a)<g(a)
(2) f(a)<g(a)
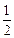 (
( ),g(a)=
),g(a)= (2) f(a)<g(a)
(2) f(a)<g(a)(1)连结AA′、BB′、CC′,
则f(a)=S△AB′C=S梯形AA′C′C-S△AA′B′-S△CC′B
=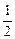 (A′A+C′C)=
(A′A+C′C)=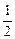 (
( ),
),
g(a)=S△A′BC′=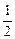 A′C′·B′B=B′B=
A′C′·B′B=B′B= 。
。


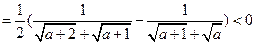
∴f(a)<g(a).
则f(a)=S△AB′C=S梯形AA′C′C-S△AA′B′-S△CC′B
=
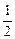 (A′A+C′C)=
(A′A+C′C)=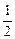 (
( ),
),g(a)=S△A′BC′=
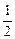 A′C′·B′B=B′B=
A′C′·B′B=B′B= 。
。 


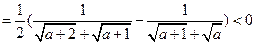
∴f(a)<g(a).

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
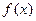 =a
=a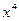 +b
+b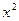 +c的图像经过点(0,1),且在
+c的图像经过点(0,1),且在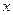 =1处的切线方程是y=
=1处的切线方程是y=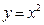 的图象,求出其在点
的图象,求出其在点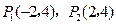 处的切线方程,并画出切线.
处的切线方程,并画出切线.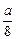 .
. 
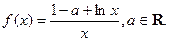
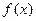 的极值;
的极值;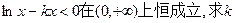 的取值范围;
的取值范围;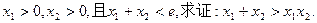

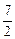 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M处法线的斜率为-
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M处法线的斜率为-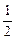 ,则点M的坐标为______.
,则点M的坐标为______.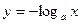 在点
在点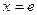 处的切线与直线
处的切线与直线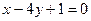 垂直,则实数
垂直,则实数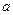 等于( )
等于( )