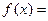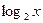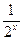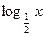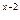题目内容
已知抛物线C:y=x2＋4x＋
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M处法线的斜率为－
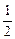,则点M的坐标为______.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M处法线的斜率为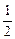－,则点M的坐标为______.(－1, )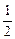
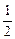)本题考查导数的几何意义.抛物线上某点处切线的斜率即为其导数.
抛物线C的函数表达式y=x2＋4x＋的导数y′=2x＋4,
C上点(x0,y0)处切线的斜率k0=2x0＋4.
∵过点(x0,y0)的法线斜率为－,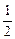
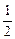∴－(2x0＋4)=－1.
解得x0=－1,y0=,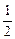
故点M的坐标为(－1,).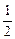
抛物线C的函数表达式y=x2＋4x＋
的导数y′=2x＋4,C上点(x0,y0)处切线的斜率k0=2x0＋4.
∵过点(x0,y0)的法线斜率为－
,∴－
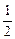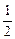(2x0＋4)=－1.解得x0=－1,y0=
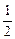,故点M的坐标为(－1,
).
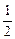练习册系列答案
相关题目
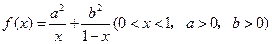的最值。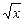
的图像上，它们的横坐标分别是a、a+1、a+2
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).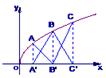 
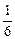处的切线的倾斜角是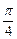
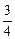π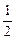
x2－2x在点(1,－
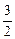)处的切线的倾斜角为__________.
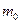的水滴，在重力的作用下下落，由于蒸发而减少质量，并且减少的质量与时间成正比（比例常数为
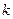），从它下落开始经过多少秒时，动能达到最大？动能的最大值为多少？
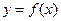是函数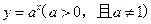
的反函数，且
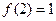，则
