题目内容
已知f(x)是偶函数而且在(0,+∞)上是减函数,判断f(x)在(-∞,0)上的增减性并加以证明.
函数f(x)在(-∞,0)上是增函数
函数f(x)在(-∞,0)上是增函数,设x1<x2<0,因为f(x)是偶函数,所以f(-x1)=f(x1),f(-x2)=f(x2),由假设可知-x1>-x2>0,又已知f(x)在(0,+∞)上是减函数,于是有f(-x1)<f(-x2),即f(x1)<f(x2),由此可知,函数f(x)在(-∞,0)上是增函数.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
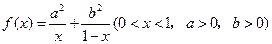 的最值。
的最值。 为曲线
为曲线 在点(1,0)处的切线,直线
在点(1,0)处的切线,直线 为该曲线的另一条切线,且
为该曲线的另一条切线,且

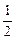 x2(万元)(0≤x≤5),其中x是产品售出的数量(单位: 百台)
x2(万元)(0≤x≤5),其中x是产品售出的数量(单位: 百台)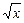 的图像上,它们的横坐标分别是a、a+1、a+2
的图像上,它们的横坐标分别是a、a+1、a+2 又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a). 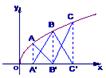
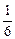 处的切线的倾斜角是
处的切线的倾斜角是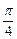
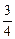 π
π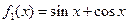 ,记
,记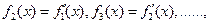
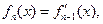
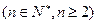 ,则
,则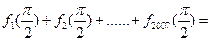 ________.
________.