题目内容
若曲线y=－x3＋3与直线y=－6x＋b相切，则b为
A．3＋4 | B．4±3 |
| C．4－3 | D．3±4 |
D
本题考查导数的几何意义.由函数在某点处导数为－b,构造关于b的方程.
y′=－3x2,令y′=－3x2=－6,得x1=－或x2=，即曲线在x1=－或x2=处切线斜率为－6.
把x1、x2分别代入曲线y=－x3＋3中得y1=3＋2,y2=3－2.
所以两个切点为(－,3＋2),(,3－2).
把两个点的坐标分别代入直线y=－6x＋b，得b1=3－4,b2=3＋4.
y′=－3x2,令y′=－3x2=－6,得x1=－
或x2=，即曲线在x1=－或x2=处切线斜率为－6.把x1、x2分别代入曲线y=－x3＋3中得y1=3＋2
,y2=3－2.所以两个切点为(－
,3＋2),(,3－2).把两个点的坐标分别代入直线y=－6x＋b，得b1=3－4
,b2=3＋4.
练习册系列答案
相关题目
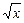的图像上，它们的横坐标分别是a、a+1、a+2
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).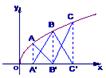 
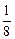t2,则t=2时，此木块在水平方向的瞬时速度为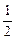
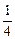
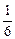处的切线的倾斜角是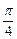
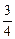π
x2－2x在点(1,－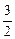
)处的切线的倾斜角为__________.
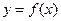在定义域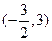
内可导，其图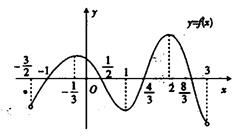
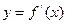，则不等式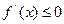
的解集为_____________