题目内容
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|= ![]() |PQ|. (Ⅰ)求C的方程;
|PQ|. (Ⅰ)求C的方程;
(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.
【答案】解:(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C:y2=2px(p>0),
可得x0= ![]() ,∵点P(0,4),∴|PQ|=
,∵点P(0,4),∴|PQ|= ![]() .
.
又|QF|=x0+ ![]() =
= ![]() +
+ ![]() ,|QF|=
,|QF|= ![]() |PQ|,
|PQ|,
∴ ![]() +
+ ![]() =
= ![]() ×
× ![]() ,求得 p=2,或 p=﹣2(舍去).
,求得 p=2,或 p=﹣2(舍去).
故C的方程为 y2=4x.
(Ⅱ)由题意可得,直线l和坐标轴不垂直,y2=4x的焦点F(1,0),
设l的方程为 x=my+1(m≠0),
代入抛物线方程可得y2﹣4my﹣4=0,显然判别式△=16m2+16>0,y1+y2=4m,y1y2=﹣4.
∴AB的中点坐标为D(2m2+1,2m),弦长|AB|= ![]() |y1﹣y2|=
|y1﹣y2|= ![]() =4(m2+1).
=4(m2+1).
又直线l′的斜率为﹣m,∴直线l′的方程为 x=﹣ ![]() y+2m2+3.
y+2m2+3.
过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,
把线l′的方程代入抛物线方程可得 y2+ ![]() y﹣4(2m2+3)=0,∴y3+y4=
y﹣4(2m2+3)=0,∴y3+y4= ![]() ,y3y4=﹣4(2m2+3).
,y3y4=﹣4(2m2+3).
故线段MN的中点E的坐标为( ![]() +2m2+3,
+2m2+3, ![]() ),∴|MN|=
),∴|MN|= ![]() |y3﹣y4|=
|y3﹣y4|= 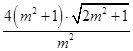 ,
,
∵MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|= ![]() |MN|,
|MN|,
∴ ![]() +DE2=
+DE2= ![]() MN2,
MN2,
∴4(m21)2 + ![]() +
+ ![]() =
= ![]() ×
× ![]() ,化简可得 m2﹣1=0,
,化简可得 m2﹣1=0,
∴m=±1,∴直线l的方程为 x﹣y﹣1=0,或 x+y﹣1=0
【解析】(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C的方程,求得x0= ![]() ,根据|QF|=
,根据|QF|= ![]() |PQ|求得 p的值,可得C的方程.(Ⅱ)设l的方程为 x=my+1 (m≠0),代入抛物线方程化简,利用韦达定理、中点公式、弦长公式求得弦长|AB|.把直线l′的方程代入抛物线方程化简,利用韦达定理、弦长公式求得|MN|.由于MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|=
|PQ|求得 p的值,可得C的方程.(Ⅱ)设l的方程为 x=my+1 (m≠0),代入抛物线方程化简,利用韦达定理、中点公式、弦长公式求得弦长|AB|.把直线l′的方程代入抛物线方程化简,利用韦达定理、弦长公式求得|MN|.由于MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|= ![]() |MN|,由此求得m的值,可得直线l的方程.
|MN|,由此求得m的值,可得直线l的方程.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案【题目】为了稳定市场,确保农民增收,某农产品7个月份的每月市场收购价格与其前三个月的市场收购价格有关,并使其与前三个月的市场收购价格之差的平方和最小,下表列出的是该产品今年前6个月的市场收购价格,则前7个月该产品的市场收购价格的方差为( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
价格(元/担) | 68 | 78 | 67 | 71 | 72 | 70 |
A.![]()
B.![]()
C.11
D.![]()