题目内容
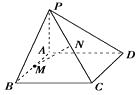
【题目】如图, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是
是 ![]() 的直径,
的直径, ![]() 是底面圆周上异于
是底面圆周上异于 ![]() 的任意一点,
的任意一点, ![]() ,
, ![]() .
.
(1)求证: ![]()
(2)当三棱锥 ![]() 的体积最大时,求
的体积最大时,求 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一点
上是否存在一点 ![]() ,使二面角
,使二面角 ![]() 的平面角为45°?若存在,求出此时
的平面角为45°?若存在,求出此时 ![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】
(1)解:∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]()
∴ ![]() ,又
,又 ![]() ,
, ![]()
∴ ![]() 平面
平面 ![]()
又∵ ![]() 平面
平面 ![]() ,
,
∴平面 ![]() 平面
平面 ![]() ,
,
而平面 ![]() 平面
平面 ![]() ,
, ![]()
∴ ![]() 平面
平面 ![]() ,而
,而 ![]() 平面
平面 ![]() ,
,
∴ ![]()
(2)解:设 ![]() ,在
,在 ![]() 中,
中, ![]()
∵ ![]() 平面
平面 ![]() ,
,
∴ ![]() 是三棱锥
是三棱锥 ![]() 的高
的高
因此三棱锥 ![]() 的体积为
的体积为![]()
![]()
![]()
∵ ![]() ,
, ![]() ,
,
∴当 ![]() ,即
,即 ![]() 时,三棱锥
时,三棱锥 ![]() 体积的最大值为
体积的最大值为 ![]()
此时 ![]() 为等腰直角三角形,
为等腰直角三角形,
∴ ![]() 与平面
与平面 ![]() 所成角度为45°
所成角度为45°
(3)解:存在这样的点 ![]() 且
且 ![]() ,理由如下:
,理由如下:
记 ![]() 的中点为
的中点为 ![]() ,连接
,连接 ![]() ,
,
∵ ![]() 为等腰直角三角形
为等腰直角三角形
∴ ![]() ,由(1)知
,由(1)知 ![]() ,
, ![]()
∴ ![]() 平面
平面 ![]() ,
,
又 ![]() 平面
平面 ![]() ,∴
,∴ ![]()
∴ ![]() 是二面角
是二面角 ![]() 的平面角,即
的平面角,即 ![]()
![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,
,
∴ ![]()
在 ![]() 中,
中, ![]()
在 ![]() 和
和 ![]() 中,可解得
中,可解得 ![]() ,
, ![]()
【解析】(1)根据圆的直径所对圆周角为直角,以及SA与平面ABC垂直的性质,得到直线BC与平面SAC垂直,证明平面SBC与平面SAC垂直,再利用线面垂直的性质证明结论。
(2)设 AC=x ,用x表示出三棱锥S-ABC的体积,利用二次函数的最值问题,求出结果。
(3)取SB的中点E,分别连接AE,DE,根据AD与平面SBC垂直,AD与SB垂直,证明SB与平面ADE垂直,证明 是二面角 A-SB-C 的平面角,求出结果。

 阅读快车系列答案
阅读快车系列答案【题目】一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?