Question

【题目】若不等式2xlogax<0在x∈ 上恒成立，求实数a的取值范围．

Answer 1

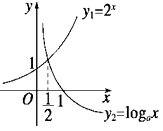
【答案】解：要使不等式2x<logax在x∈ 上恒成立，则函数y＝logax的图象在 内恒在函数y＝2x图象的上方，而y＝2x的图象过点 .由图可知， ，显然这里0<a<1，∴函数y＝logax递减．又 ，∴ ，即 ，∴所求的实数a的取值范围为 .

【解析】将不等式恒成立转化为不等式两边的函数中,一个函数图恒在另一个函数图象的上方求解参数的范围.
【考点精析】通过灵活运用指数函数的图像与性质，掌握a0=1, 即x=0时，y=1，图象都经过(0，1)点;ax=a，即x=1时，y等于底数a;在0<a<1时:x<0时，ax>1,x>0时，0<ax<1;在a>1时:x<0时,0<ax<1,x>0时，ax>1即可以解答此题．