题目内容
13.函数f(x)=1-3sin2x的最小正周期为π.分析 由条件利用半角公式化简函数的解析式,再利用余弦函数的周期性求得函数的最小正周期.
解答 解:∵函数f(x)=1-3sin2x=1-3$\frac{1-cos2x}{2}$=-$\frac{1}{2}$+$\frac{3}{2}$cos2x,
∴函数的最小正周期为$\frac{2π}{2}$=π,
故答案为:π.
点评 本题主要考查半角公式的应用,余弦函数的周期性,属于基础题.

练习册系列答案
相关题目
3.已知正项等比数列{an}满足a7=a6+2a5,若am,an满足$\sqrt{{a}_{m}{a}_{n}}$=8a1,则$\frac{1}{m}$+$\frac{9}{n}$的最小值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
1.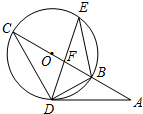 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
下列结论中,错误的是( )
 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的下列结论中,错误的是( )
| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |