题目内容
1. 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
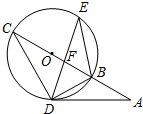
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的下列结论中,错误的是( )
| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |
分析 对四个选项分别进行判断,即可得出结论.
解答 解:由切割线定理可得AD2=AB•AC,即12=AB•(AB+4),所以AB=2,故A正确;
由相交弦定理可得BF•CF=DF•EF,故可得B正确;
由△ABD∽△ADC,可得$\frac{BD}{DC}=\frac{AB}{AD}=\frac{\sqrt{3}}{3}$,因为BC=4,所以DC=23,所以∠C=30°,所以∠E=30°,故C正确;
△EBD、△CDB中只有一对角相等,不可推出△EBD∽△CDB,故不正确.
故选:D.
点评 本题考查切割线定理、相交弦定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
9.甲、乙两人在2015年1月至5月的纯收入(单位:千元)的数据如下表:
(1)由表中数据直观分析,甲、乙两人中谁的纯收入较稳定?
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
16.已知偶函数f(x),当x∈[0,2)时,f(x)=2sinx,当x∈[2,+∞)时,f(x)=log2x,则$f({-\frac{π}{3}})+f(4)$=( )
| A. | $\sqrt{3}+2$ | B. | 1 | C. | 3 | D. | $-\sqrt{3}+2$ |
10.设 Pn(xn,yn)是直线2x-y=$\frac{n}{n+1}$(n∈N*)与圆x2+y2=2在第一象限的交点,则极限$\lim_{n→∞}\frac{{{y_n}-1}}{{{x_n}-1}}$=( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
1.给出下列两个推理:
①在△ABC中,若D为BC的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),由此推测:在空间四面体ABCD中,若M为△BCD的重心,则$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$).
②无根不循环小数都是无理数,因为e=2.7182818459045…是无限不循环小数,所以e是无理数.
对于上述两个推理,下列判断正确的是( )
①在△ABC中,若D为BC的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),由此推测:在空间四面体ABCD中,若M为△BCD的重心,则$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$).
②无根不循环小数都是无理数,因为e=2.7182818459045…是无限不循环小数,所以e是无理数.
对于上述两个推理,下列判断正确的是( )
| A. | ①是类比推理,②是归纳推理 | B. | ①是类比推理,②是演绎推理 | ||
| C. | ①是归纳推理,②是演绎推理 | D. | ①是演绎推理,②是类比推理 |