题目内容
12.已知f(x)=$\frac{1}{3}$x3+ax2+x为奇函数,则y=f(x)在x=1处的切线与两坐标轴围成的三角形面积为$\frac{1}{9}$.分析 由奇函数的定义,可得a=0,求得f(x)的导数,求得切线的斜率和切点,由点斜式方程可得切线方程,求得x,y轴上的截距,由三角形的面积公式计算即可得到.
解答 解:f(x)=$\frac{1}{3}$x3+ax2+x为奇函数,
即有f(-x)=-f(x),
-$\frac{1}{3}$x3+ax2-x=-$\frac{1}{3}$x3-ax2-x,
可得a=0,
即f(x)=$\frac{1}{3}$x3+x,导数f′(x)=x2+1,
则y=f(x)在x=1处的切线斜率为f′(1)=2,
切点为(1,$\frac{4}{3}$),
即有切线方程为y-$\frac{4}{3}$=2(x-1),
令x=0,可得y=-$\frac{2}{3}$,
令y=0,可得x=$\frac{1}{3}$.
则切线与两坐标轴围成的三角形面积为$\frac{1}{2}$×$\frac{1}{3}$×$\frac{2}{3}$=$\frac{1}{9}$.
故答案为:$\frac{1}{9}$.
点评 本题考查导数的运用:求切线方程,主要考查导数的几何意义,同时考查函数的奇偶性的定义和直线的点斜式方程和三角形的面积的计算,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
10.设 Pn(xn,yn)是直线2x-y=$\frac{n}{n+1}$(n∈N*)与圆x2+y2=2在第一象限的交点,则极限$\lim_{n→∞}\frac{{{y_n}-1}}{{{x_n}-1}}$=( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
17.以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为$\left\{\begin{array}{l}x=3-t\\ y=t-5\end{array}\right.$(t为参数),圆C的极坐标方程为ρ=4(cosθ+sinθ),则圆C上的点到直线l的距离的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
1.给出下列两个推理:
①在△ABC中,若D为BC的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),由此推测:在空间四面体ABCD中,若M为△BCD的重心,则$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$).
②无根不循环小数都是无理数,因为e=2.7182818459045…是无限不循环小数,所以e是无理数.
对于上述两个推理,下列判断正确的是( )
①在△ABC中,若D为BC的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),由此推测:在空间四面体ABCD中,若M为△BCD的重心,则$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$).
②无根不循环小数都是无理数,因为e=2.7182818459045…是无限不循环小数,所以e是无理数.
对于上述两个推理,下列判断正确的是( )
| A. | ①是类比推理,②是归纳推理 | B. | ①是类比推理,②是演绎推理 | ||
| C. | ①是归纳推理,②是演绎推理 | D. | ①是演绎推理,②是类比推理 |
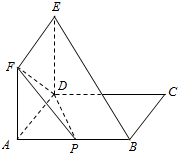 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.