题目内容
4．已知{an}是递增等差数列，a1=2，且a1，a2，a5成等比数列，则此数列的公差d=4．分析 设出公差，利用已知条件列出方程求解即可．
解答 解：设等差数列的公差为d，依题意，2，2+d，2+4d成等比数列，∴（2+d）2=2（2+4d），解得d=0（舍去）或d=4．
故答案为：4．
点评 本题考查等差数列以及等比数列的应用，基本知识的考查．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
14．
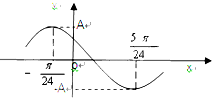已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如下图所示，且直线y=A与曲线y=f（x）（-$\frac{π}{24}$$≤x≤\frac{11π}{24}$）所围成的封闭图形的面积为π，则f（$\frac{π}{8}$）+f（$\frac{2π}{8}$）+f（$\frac{3π}{8}$）+…+f（$\frac{2015π}{8}）$的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如下图所示，且直线y=A与曲线y=f（x）（-$\frac{π}{24}$$≤x≤\frac{11π}{24}$）所围成的封闭图形的面积为π，则f（$\frac{π}{8}$）+f（$\frac{2π}{8}$）+f（$\frac{3π}{8}$）+…+f（$\frac{2015π}{8}）$的值为（ ）| A． | -$\sqrt{3}$ | B． | -1-$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | -1+$\sqrt{3}$ |
19．已知平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，y），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则y=（ ）
| A． | -1 | B． | 1 | C． | -4 | D． | 4 |
9．甲、乙两人在2015年1月至5月的纯收入（单位：千元）的数据如下表：
（1）由表中数据直观分析，甲、乙两人中谁的纯收入较稳定？
（2）求y关于x的线性回归方程，并预测甲在6月份的纯收入；
（3）现从乙这5个月的纯收入中，随机抽取两个月，求恰有1个月的纯收入在区间（3，3.5）中的概率．
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
（2）求y关于x的线性回归方程，并预测甲在6月份的纯收入；
（3）现从乙这5个月的纯收入中，随机抽取两个月，求恰有1个月的纯收入在区间（3，3.5）中的概率．
16．已知偶函数f（x），当x∈[0，2）时，f（x）=2sinx，当x∈[2，+∞）时，f（x）=log2x，则$f（{-\frac{π}{3}}）+f（4）$=（ ）
| A． | $\sqrt{3}+2$ | B． | 1 | C． | 3 | D． | $-\sqrt{3}+2$ |
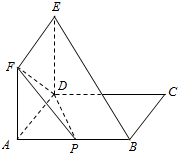如图所示：矩形ABCD与正方形ADEF所在的平面互相垂直，AB=2AD=4，点P为AB的中点．