题目内容
3.已知正项等比数列{an}满足a7=a6+2a5,若am,an满足$\sqrt{{a}_{m}{a}_{n}}$=8a1,则$\frac{1}{m}$+$\frac{9}{n}$的最小值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 由等比数列的性质易得m+n=8,可得$\frac{1}{m}$+$\frac{9}{n}$=$\frac{1}{8}$($\frac{1}{m}$+$\frac{9}{n}$)(m+n)=$\frac{1}{8}$(10+$\frac{n}{m}$+$\frac{9m}{n}$),由基本不等式求最值可得.
解答 解:∵正项等比数列{an}满足a7=a6+2a5,
∴q2a5=qa5+2a5,即q2-q-2=0,
解得公比q=2,或q=-1(舍去)
又∵am,an满足$\sqrt{{a}_{m}{a}_{n}}$=8a1,
∴aman=64a12,∴qm+n-2a12=64a12,
∴qm+n-2=64,∴m+n-2=6,即m+n=8,
∴$\frac{1}{m}$+$\frac{9}{n}$=$\frac{1}{8}$($\frac{1}{m}$+$\frac{9}{n}$)(m+n)=$\frac{1}{8}$(10+$\frac{n}{m}$+$\frac{9m}{n}$)
≥$\frac{1}{8}$(10+2$\sqrt{\frac{n}{m}•\frac{9m}{n}}$)=2
当且仅当$\frac{n}{m}$=$\frac{9m}{n}$即m=2且n=6时取等号,
故选:A.
点评 本题考查基本不等式求最值,涉及等比数列的通项公式,属基础题.

练习册系列答案
相关题目
14.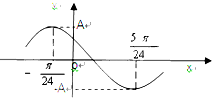 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )| A. | -$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -1+$\sqrt{3}$ |
18.已知x、y满足约束条件$\left\{\begin{array}{l}x+y-1≤0\\ x-y≤0\\ x≥0\end{array}\right.$则 z=x+2y 的最大值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
8.设集合A={x|x2-6x+8<0},B={x|2<2x<8},则A∩B=( )
| A. | {x|1<x<4} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|3<x<4} |