题目内容
如图1,在直角梯形 中,
中, ,
, ,
, .将
.将 沿
沿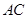 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(1)求证: ⊥平面
⊥平面 ;(2)求几何体
;(2)求几何体 的体积.
的体积.

 中,
中, ,
, ,
, .将
.将 沿
沿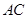 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.(1)求证:
 ⊥平面
⊥平面 ;(2)求几何体
;(2)求几何体 的体积.
的体积.
(1)详见解析
(2)几何体 的体积为
的体积为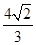
(2)几何体
 的体积为
的体积为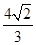
(1)在图1中,可得
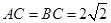 ,从而
,从而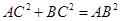 ,故
,故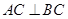
取
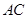 中点
中点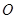 连结
连结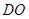 ,则
,则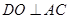 ,又面
,又面
 面
面 ,
,面

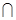 面
面
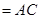 ,
,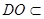 面
面 ,从而
,从而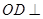 平面
平面 ,
,∵
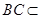 面
面 ,∴
,∴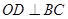
又
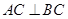 ,
,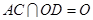 ,
,∴
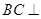 平面
平面
解:在图1中,可得
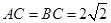 ,从而
,从而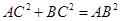 ,故
,故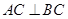
∵面

 面
面 ,面
,面
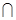 面
面
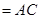 ,
,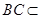 面
面 ,从而
,从而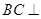 平面
平面
(2)由(1)可知
 为三棱锥
为三棱锥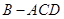 的高.
的高. 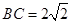 ,
,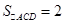
所以
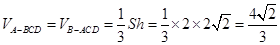
∴几何体
 的体积为
的体积为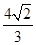

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 中,
中, 平面
平面 .
.
 平面
平面 ;
; ,
,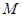 为
为 中点,求三棱锥
中点,求三棱锥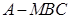 的体积.
的体积. 的边长为2,沿着
的边长为2,沿着 上的高
上的高 将正三角形折起,使得平面
将正三角形折起,使得平面 平面
平面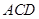 ,则三棱锥
,则三棱锥 的体积是
的体积是  的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是 .
的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是 . 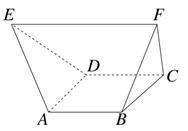




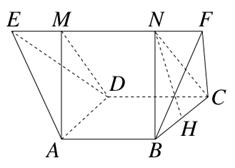
 中,
中, ,
, ,直线
,直线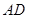 与底面
与底面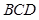 所成角为
所成角为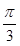 ,则此时三棱锥外接球的表面积为( )
,则此时三棱锥外接球的表面积为( )



 .
.