题目内容
(本小题满分12分)
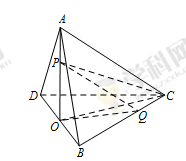
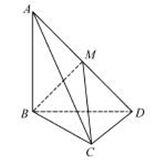
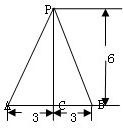
如图,三棱锥 中,
中, 平面
平面 .
.

(1)求证: 平面
平面 ;
;
(2)若 ,
, 为
为 中点,求三棱锥
中点,求三棱锥 的体积.
的体积.
如图,三棱锥
 中,
中, 平面
平面 .
.
(1)求证:
 平面
平面 ;
;(2)若
 ,
, 为
为 中点,求三棱锥
中点,求三棱锥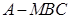 的体积.
的体积.(1)见解析.(2)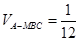 .
.
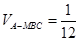 .
.试题分析:
(1)由
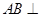 平面BCD,
平面BCD,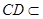 平面BCD,
平面BCD,得到
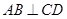 .
.进一步即得
 平面
平面 .
.(2)思路一:由
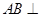 平面BCD,得
平面BCD,得 .
.确定
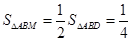 .
.根据
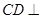 平面ABD,
平面ABD,知三棱锥C-ABM的高
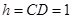 ,
,得到三棱锥
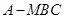 的体积
的体积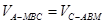 .
.思路二:由
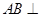 平面BCD知,平面ABD
平面BCD知,平面ABD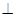 平面BCD,
平面BCD,根据平面ABD
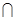 平面BCD=BD,
平面BCD=BD,通过过点M作
 交BD于点N.
交BD于点N.得到
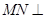 平面BCD,且
平面BCD,且 ,
,利用
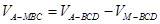 计算三棱锥
计算三棱锥 的体积.
的体积.试题解析:解法一:
(1)∵
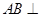 平面BCD,
平面BCD,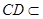 平面BCD,
平面BCD,∴
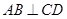 .
.又∵
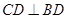 ,
,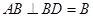 ,
,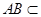 平面ABD,
平面ABD,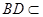 平面ABD,
平面ABD,∴
 平面
平面 .
.(2)由
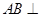 平面BCD,得
平面BCD,得 .
.∵
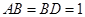 ,∴
,∴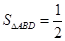 .
.∵M是AD的中点,
∴
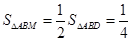 .
.由(1)知,
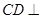 平面ABD,
平面ABD,∴三棱锥C-ABM的高
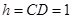 ,
,因此三棱锥
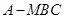 的体积
的体积 .
.
解法二:
(1)同解法一.
(2)由
 平面BCD知,平面ABD
平面BCD知,平面ABD 平面BCD,
平面BCD,又平面ABD
 平面BCD=BD,
平面BCD=BD,如图,过点M作
 交BD于点N.
交BD于点N.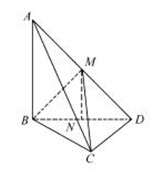
则
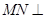 平面BCD,且
平面BCD,且 ,
,又
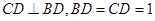 ,
,∴
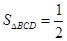 .
.∴三棱锥
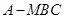 的体积
的体积 .
.
练习册系列答案
相关题目
 中,
中, 平面
平面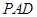 ,
, ,
, ,
, 是
是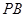 的中点,
的中点, 是
是 上的点且
上的点且 ,
, 为△
为△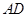 边上的高.
边上的高.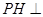 平面
平面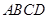 ;
; ,
, ,
, ,求三棱锥
,求三棱锥 的体积;
的体积;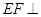 平面
平面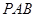 .
.
 中,
中, ,
, ,
, .将
.将 沿
沿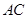 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示. ⊥平面
⊥平面 ;(2)求几何体
;(2)求几何体 的体积.
的体积.
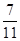
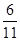
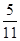
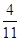
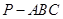 中,
中, ,
,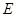 分别为
分别为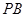 ,
,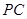 的中点,记三棱锥
的中点,记三棱锥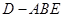 的体积为
的体积为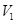 ,
,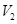 ,则
,则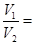 ________.
________. 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边 、
、 上,且
上,且 ,
, ,将此正
,将此正 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥 的体积是( )
的体积是( )



 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.  ,求
,求 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
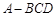 中,
中,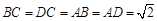 ,
,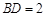 ,平面
,平面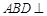 平面
平面 ,
,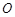 为
为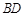 中点,点
中点,点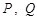 分别为线段
分别为线段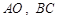 上的动点(不含端点),且
上的动点(不含端点),且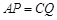 ,则三棱锥
,则三棱锥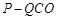 体积的最大值为________.
体积的最大值为________.