题目内容
已知正三角形 的边长为2,沿着
的边长为2,沿着 上的高
上的高 将正三角形折起,使得平面
将正三角形折起,使得平面 平面
平面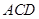 ,则三棱锥
,则三棱锥 的体积是
的体积是
 的边长为2,沿着
的边长为2,沿着 上的高
上的高 将正三角形折起,使得平面
将正三角形折起,使得平面 平面
平面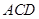 ,则三棱锥
,则三棱锥 的体积是
的体积是 
试题分析:∵AD⊥BD,AD⊥CD,BD∩CD=D,∴AD⊥平面BCD,
∵平面ABD⊥平面ACD,且∠BDC是二面角B-AD-C的平面角
∴∠BDC=90°,∵AD是边长为2的正三角形的高,可得BD=CD=1,AD=

∴△BCD的面积S△BCD=
 ×1×1=
×1×1=
因此三棱锥A-BCD的体积V=
 ×S△BCD×AD=
×S△BCD×AD= ×
× ×
× =
=
故答案为:


练习册系列答案
相关题目
 中,
中, 平面
平面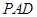 ,
, ,
, ,
, 是
是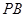 的中点,
的中点, 是
是 上的点且
上的点且 ,
, 为△
为△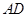 边上的高.
边上的高.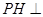 平面
平面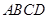 ;
; ,
, ,
, ,求三棱锥
,求三棱锥 的体积;
的体积;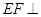 平面
平面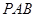 .
.
 中,
中, ,
, ,
, .将
.将 沿
沿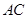 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示. ⊥平面
⊥平面 ;(2)求几何体
;(2)求几何体 的体积.
的体积.
 中,平面
中,平面 平面
平面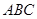 ,
, 于点
于点 ,且
,且 ,
, ,
, 

 ,
, ,求三棱锥
,求三棱锥
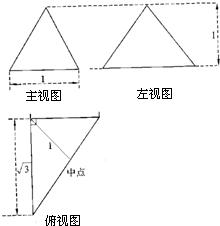






 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边 、
、 上,且
上,且 ,
, ,将此正
,将此正 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥 的体积是( )
的体积是( )


