题目内容
15.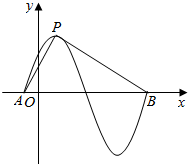 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )| A. | $\frac{4}{7}$ | B. | $\frac{8}{7}$ | C. | 6 | D. | 8 |
分析 求出函数的周期,与最值,过P作PD⊥x轴于D,求出∠APD与∠BPD的正切,利用两角和的正切函数求出tan∠APB.
解答 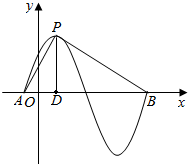 解:由题意可知函数的周期T=$\frac{2π}{π}=2$,
解:由题意可知函数的周期T=$\frac{2π}{π}=2$,
最大值为1,
过P作PD⊥x轴于D,
则AD=$\frac{1}{2}$,DB=$\frac{3}{2}$,DP=1,
则tan∠APD=$\frac{1}{2}$,tan∠BPD=$\frac{3}{2}$,
故tan∠APB=tan(∠APD+∠BPD)=$\frac{\frac{1}{2}+\frac{3}{2}}{1-\frac{1}{2}×\frac{3}{2}}$=8.
故选:D.
点评 本题考查三角函数的图象与两角和的正切函数公式的应用,考查理解能力计算能力.

练习册系列答案
相关题目
6.$\int_{-1}^1{\sqrt{1-{x^2}}dx}$等于( )
| A. | 1 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
3.直线2y+2x-5=0的倾斜角是( )
| A. | 45° | B. | 135° | C. | 120° | D. | 150° |
10.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程x3+x2-2x-2=0的一个近似根可以为(精度为0.1)( )
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
| A. | 1.2 | B. | 1.3 | C. | 1.43 | D. | 1.5 |
20. 某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
 某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )| A. | $\frac{8π}{3}$ | B. | $\frac{16π}{3}$ | C. | 16π | D. | 8π |