题目内容
3．直线2y+2x-5=0的倾斜角是（ ）| A． | 45° | B． | 135° | C． | 120° | D． | 150° |
分析 由直线方程求出斜率，再由斜率公式求出直线的倾斜角．
解答 解：由题意知，直线方程是：2y+2x-5=0，
∴直线2y+2x-5=0的斜率k=-1，
由k=tanα得，则直线的倾斜角是135°，
故选：B．
点评 本题考查由直线方程求出直线的斜率、倾斜角，以及斜率公式，属于基础题．
练习册系列答案
相关题目
13．已知幂函数f（x）=（m-1）2x${\;}^{{m}^{2}-4m+2}$在（0，+∞）上单调递增，函数g（x）=2x-k，当x∈[1，2）时，记f（x），g（x）的值域分别为集合A，B，若A∪B=A，则实数k的取值范围是（ ）
| A． | （0，1） | B． | [0，1） | C． | （0，1] | D． | [0，1] |
14．离散型随机变量X的分布列如表，且E（X）=2，则D（2X-3）=4
| X | 0 | 2 | a |
| P | $\frac{1}{6}$ | p | $\frac{1}{3}$ |
8．由直线x-y+1=0，x+y-5=0和x-1=0所围成的三角形区域（包括边界）用不等式组可表示为（ ）
| A． | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≥0}\\{x≤1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≤1}\end{array}\right.$ |
15．
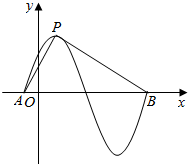函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高，A，B是图象与x轴的交点，则tan∠APB等于（ ）
函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高，A，B是图象与x轴的交点，则tan∠APB等于（ ）| A． | $\frac{4}{7}$ | B． | $\frac{8}{7}$ | C． | 6 | D． | 8 |
9．执行如图所示的程序框图，则输出的结果是（ ）
| A． | 6 | B． | -6 | C． | 5 | D． | -5 |