题目内容
10．若函数f（x）=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算，参考数据如下表：| f（1）=-2 | f（1.5）=0.625 |
| f（1.25）=-0.984 | f（1.375）=-0.260 |
| f（1.438）=0.165 | f（1.4065）=-0.052 |
| A． | 1.2 | B． | 1.3 | C． | 1.43 | D． | 1.5 |
分析 由根的存在性定理得出f（x）在（1.4065，1.438）内有零点，再由题意求出符合条件的方程f（x）=0的近似根．
解答 解：∵f（1.438）=0.165＞0，
f（1.4065）=-0.052＜0，
∴函数f（x）在（1.4065，1.438）内存在零点，
又1.438-1.406 5＜0.1，
结合选项知1.43为方程f（x）=0的一个近似根．
故选：C．
点评 本题考查了函数零点的应用问题，也考查了求方程近似根的应用问题，是基础题目．
练习册系列答案
相关题目
5．已知数列{an}（n=1，2，3，4，5）满足a1=a5=0，且当2≤k≤5时，（ak-ak-1）2=1，令S=$\sum_{i=1}^5{a_i}$，则S不可能的值是（ ）
| A． | 4 | B． | 0 | C． | 1 | D． | -4 |
15．
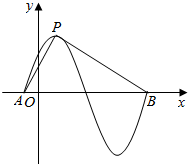函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高，A，B是图象与x轴的交点，则tan∠APB等于（ ）
函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高，A，B是图象与x轴的交点，则tan∠APB等于（ ）| A． | $\frac{4}{7}$ | B． | $\frac{8}{7}$ | C． | 6 | D． | 8 |
2．为了得到函数y=cos（$\frac{x}{5}$$+\frac{1}{3}$）（x∈R）的图象，只需把余弦曲线上所有的点（ ）
| A． | 先向左平行移动$\frac{1}{3}$个单位长度，再把所得图象上所有的点的横坐标伸长到原来的5倍（纵坐标不变） | |
| B． | 先向左平行移动$\frac{π}{3}$个单位长度，再把所得图象上所有的点的横坐标伸长到原来的5倍（纵坐标不变） | |
| C． | 先向右平行移动$\frac{1}{3}$个单位长度，再把所得图象上所有的点的横坐标缩短到原来的$\frac{1}{5}$倍（纵坐标不变） | |
| D． | 先向右平行移动$\frac{π}{3}$个单位长度，再把所得图象上所有的点的横坐标缩短到原来的$\frac{1}{5}$倍（纵坐标不变） |
19．现有4名学生排成一排，其中甲、乙两个学生必须相邻，则不同的排法种数为（ ）
| A． | 6 | B． | 10 | C． | 12 | D． | 20 |