题目内容
4.已知f(x)=x+sinx,则${∫}_{-π}^{0}$f(x)dx=-2-$\frac{{π}^{2}}{2}$.分析 将f(x)代入,找出原函数计算即可.
解答 解:f(x)=x+sinx,则${∫}_{-π}^{0}$f(x)dx=${∫}_{-π}^{0}$(x+sinx)dx=($\frac{1}{2}{x}^{2}-cosx$)|${\;}_{-π}^{0}$=-2-$\frac{{π}^{2}}{2}$;
故答案为:-2-$\frac{{π}^{2}}{2}$.
点评 本题考查了定积分的计算,关键是找出被积函数的原函数.

练习册系列答案
相关题目
14.离散型随机变量X的分布列如表,且E(X)=2,则D(2X-3)=4
| X | 0 | 2 | a |
| P | $\frac{1}{6}$ | p | $\frac{1}{3}$ |
15.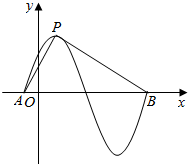 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )| A. | $\frac{4}{7}$ | B. | $\frac{8}{7}$ | C. | 6 | D. | 8 |
19.现有4名学生排成一排,其中甲、乙两个学生必须相邻,则不同的排法种数为( )
| A. | 6 | B. | 10 | C. | 12 | D. | 20 |
9.复数$\frac{2+i}{i}$(i为虚数单位)在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.执行如图所示的程序框图,则输出的结果是( )


| A. | 6 | B. | -6 | C. | 5 | D. | -5 |
10.袋中有大小相同的3个红球,7个白球,从中不放回地一次摸取2球,在已知第一次取出白球的前提下,第二次取得红球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{7}$ |