题目内容
7.对于下列命题:①将一组数据中的每个数据都加上同一个常数后,方差恒不变;
②y与x具有线性相关关系,其回归方程为$\widehat{y}$=3-5x,则y与x具有负的线性相关关系;
③在一组样本数据中的散点图中,若所有样本点(x1,y1)(i=1,2,…,n)都在直线y=$\frac{1}{2}$x+1上,则这组样本数据的样本相关系数为$\frac{1}{2}$;
④设m,n为直线,a为平面,若m∥n,m∥a,则n∥a.
其中正确命题的序号为①②(把你认为正确的命题的序号都填上).
分析 ①利用方差的公式进行判断;②利用回归方程的系数判断;③根据两个变量之间的相关系数r判断;④根据线面平行的判定定理判断.
解答 解:①将一组数据中的每个数据都加上同一个常数,数据的稳定性不变,即方差不变,①正确,
②回归直线的一次项系数为-5,y与x具有负的线性相关关系,②正确;
③由条件知这组样本数据完全正相关,其相关系数为1,③不正确;
④根据线面平行的判定定理知,一条直线在平面外,另一条在平面内,④不正确,
综上得,正确命题的序号是①②,
故答案为:①②.
点评 本题考查命题的真假判断,涉及回归直线方程的意义及性质,方差,以及线面平行的判定定理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.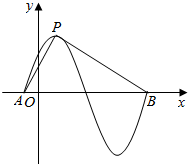 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )| A. | $\frac{4}{7}$ | B. | $\frac{8}{7}$ | C. | 6 | D. | 8 |
2.为了得到函数y=cos($\frac{x}{5}$$+\frac{1}{3}$)(x∈R)的图象,只需把余弦曲线上所有的点( )
| A. | 先向左平行移动$\frac{1}{3}$个单位长度,再把所得图象上所有的点的横坐标伸长到原来的5倍(纵坐标不变) | |
| B. | 先向左平行移动$\frac{π}{3}$个单位长度,再把所得图象上所有的点的横坐标伸长到原来的5倍(纵坐标不变) | |
| C. | 先向右平行移动$\frac{1}{3}$个单位长度,再把所得图象上所有的点的横坐标缩短到原来的$\frac{1}{5}$倍(纵坐标不变) | |
| D. | 先向右平行移动$\frac{π}{3}$个单位长度,再把所得图象上所有的点的横坐标缩短到原来的$\frac{1}{5}$倍(纵坐标不变) |
19.现有4名学生排成一排,其中甲、乙两个学生必须相邻,则不同的排法种数为( )
| A. | 6 | B. | 10 | C. | 12 | D. | 20 |
13.已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=3,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{15}$ | C. | 4 | D. | $\sqrt{13}$ |