题目内容
5.已知A(1,-2),B(2,1),且过点P(0,-1)的直线l与线段AB总有公共点,则直线l的斜率k的取值范围是[-1,1],倾斜角α的取值范围是[$\frac{3π}{4}$,π)∪[0,$\frac{π}{4}$].分析 由于直线l与连接A(1,-2)、B(2,1)的线段总有公共点,可得kPA≤kl≤kPB,再利用斜率计算公式即可得出,利用倾斜角与斜率的关系、正切函数的单调性即可得出.
解答 解:kPA=$\frac{-2+1}{1-0}$=-1,kPB=$\frac{1+1}{2}$=1.
∵直线l与连接A(1,-2)、B(2,1)的线段总有公共点,
∴kPA≤kl≤kPB,
∴-1≤k≤1.
∴直线l的斜率k的取值范围是[-1,1].
∵k=tanα,
∴-1≤tanα≤1,
∴$\frac{3π}{4}$≤a<π,0≤α≤$\frac{π}{4}$,
∴倾斜角α的取值范围是[$\frac{3π}{4}$,π)∪[0,$\frac{π}{4}$],
故答案为:[-1,1],[$\frac{3π}{4}$,π)∪[0,$\frac{π}{4}$].
点评 本题考查了直线的斜率计算公式和斜率的意义、倾斜角与斜率的关系、正切函数的单调性,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知幂函数f(x)=(m-1)2x${\;}^{{m}^{2}-4m+2}$在(0,+∞)上单调递增,函数g(x)=2x-k,当x∈[1,2)时,记f(x),g(x)的值域分别为集合A,B,若A∪B=A,则实数k的取值范围是( )
| A. | (0,1) | B. | [0,1) | C. | (0,1] | D. | [0,1] |
14.离散型随机变量X的分布列如表,且E(X)=2,则D(2X-3)=4
| X | 0 | 2 | a |
| P | $\frac{1}{6}$ | p | $\frac{1}{3}$ |
15.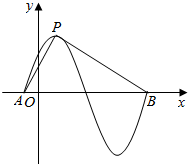 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )| A. | $\frac{4}{7}$ | B. | $\frac{8}{7}$ | C. | 6 | D. | 8 |