题目内容
20. 某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )| A. | $\frac{8π}{3}$ | B. | $\frac{16π}{3}$ | C. | 16π | D. | 8π |
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的半圆柱,求出底面面积和高,代入柱体体积公式,可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的半圆柱,
由正视图是边长为4的正方形,
可得底面直径为4,半径r=2,
其底面面积S=$\frac{1}{2}$πr2=2π,
高h=4,
故棱锥的体积V=Sh=8π,
故选:D.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.由直线x-y+1=0,x+y-5=0和x-1=0所围成的三角形区域(包括边界)用不等式组可表示为( )
| A. | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≥0}\\{x≤1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≤1}\end{array}\right.$ |
15.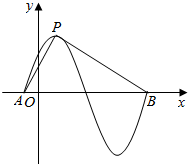 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高,A,B是图象与x轴的交点,则tan∠APB等于( )| A. | $\frac{4}{7}$ | B. | $\frac{8}{7}$ | C. | 6 | D. | 8 |
9.复数$\frac{2+i}{i}$(i为虚数单位)在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.下列四个命题中,真命题是( )
| A. | a>b,c>d⇒ac>bd | B. | a<b⇒a2<b2 | C. | $\frac{1}{a}<\frac{1}{b}$⇒a>b | D. | a>b,c<d⇒a-c>b-d |
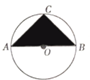 如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.
如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.