题目内容
7.下列幂函数中过点(0,0),(1,1)的偶函数是( )| A. | y=x${\;}^{\frac{1}{2}}$ | B. | y=x4 | C. | y=x-1 | D. | y=x3 |
分析 根据基本初等函数的图象与性质,对选项中的函数进行判断即可.
解答 解:对于A,y=${x}^{\frac{1}{2}}$=$\sqrt{x}$是非奇非偶的函数,∴不满足题意;
对于B,y=x4是偶函数,且过点(0,0),(1,1),满足题意;
对于C,y=x-1是奇函数,∴不满足条件;
对于D,y=x3是奇函数,∴不满足条件.
故选:B.
点评 本题考查了基本初等函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.记集合A={x|$\frac{1}{x-1}$<1},B={x|(x-1)(x+a)>0},若x∈A是x∈B的充分不必要条件,则实数a的取值范围是( )
| A. | (-2,-1] | B. | [-2,-1] | C. | ∅ | D. | [-2,+∞) |
18.函数y=$\frac{1}{3}{x^3}-{x^2}$的单调递减区间是( )
| A. | (-∞,0) | B. | (-∞,2) | C. | (2,+∞) | D. | (0,2) |
15.从同一顶点出发的三条棱长分别为1、1、$\sqrt{2}$的长方体的各顶点均在同一个球面上,则该球的体积为 ( )
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
17.下面是关于复数z=$\frac{2}{-1+i}$的四个命题:
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中真命题为( )
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
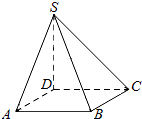 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2.