题目内容

17．下面是关于复数z=$\frac{2}{-1+i}$的四个命题：
p1：复数z对应的点在第二象限，
p2：z2=2i，
p3：z的共轭复数为1+i，
p4：z的虚部为-1．
其中真命题为（　　）
A．p2，p3B．p1，p2C．p2，p4D．p3，p4

分析 化简复数为a+bi的形式，即可利用复数的几何意义，基本运算判断选项即可．

解答 解：复数z=$\frac{2}{-1+i}$=$\frac{2（-1-i）}{（-1+i）（-1-i）}$=-1-i．
复数z对应的点（-1，-1）是在第三象限，p1不正确；
z2=（-1-i）2=2i，p2：正确；
z的共轭复数为-11+i，p3：不正确；
z的虚部为-1．p4：正确．
故选：C．

点评 本题考查复数的基本运算，复数的基本概念的应用，考查计算能力．

练习册系列答案
相关题目
7．下列幂函数中过点（0，0），（1，1）的偶函数是（　　）
A．y=x${\;}^{\frac{1}{2}}$B．y=x4C．y=x-1D．y=x3
8．两对夫妻各带一个孩子出去游玩，要站成一排照相留念，两个小孩要排在一起，两位母亲不能相邻，排法总数共有144种．（用数字作答）
5．在△ABC中，A=60°，b=1，c=2，求$\frac{a+b+c}{sinA+sinB+sinC}$=2．
12．（1）设x，y，z∈R，且满足：x2+y2+z2=1，x+2y+3z=$\sqrt{14}$，求x+y+z的值；
（2）设不等式|x-2|＜a（a∈N*）的解集为A，且$\frac{3}{2}$∈A，$\frac{1}{2}$∉A．求函数f（x）=|x+a|+|x-2|的最小值．
2．在复平面内，复数$\frac{i}{1+i}$+（1+$\sqrt{3}$i）2的共轭复数对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
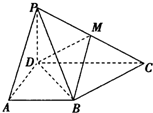9．如图所示，已知四棱锥的侧棱PD⊥平面ABCD，且底面ABCD是直角梯形，AD⊥CD，AB∥CD，AB=AD=$\frac{1}{2}$CD=2，点M是侧棱PC的中点．
（1）求证：BC⊥平面BDP；
（2）若tan∠PCD=$\frac{1}{2}$，求三棱锥M-BDP的体积．
6．已知函数f（x）=sin（ωx+φ），其中ω＞0，|φ|＜$\frac{π}{2}$．
（1）若cos（2φ-$\frac{π}{3}$）+2sin（φ-$\frac{π}{4}$）sin（φ+$\frac{π}{4}$）=$\frac{1}{2}$，求φ的值；
（2）在（1）条件下，若函数f（x）图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$，求函数的解析式，并求最小正实数m，使得函数f（x）的图象向左平移m个单位所得对应的函数是奇函数．
7．等差数列{an}{bn}的前n项和分别为Sn，Tn，$\frac{{S}_{n}}{{T}_{n}}$=$\frac{3n}{3n+1}$，则$\frac{{a}_{n}}{{b}_{n}}$=$\frac{6n-3}{6n-2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网