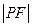题目内容
已知点A(2,8),B(x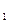 ,y
,y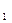 ),C(x
),C(x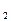 ,y
,y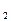 )在抛物线y
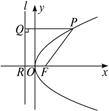
)在抛物线y =2px上,△ABC的重心与此抛物线的焦点F重合(如图)。
=2px上,△ABC的重心与此抛物线的焦点F重合(如图)。
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标。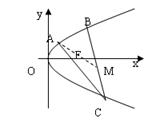
 ,y
,y ),C(x
),C(x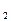 ,y
,y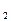 )在抛物线y
)在抛物线y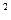 =2px上,△ABC的重心与此抛物线的焦点F重合(如图)。
=2px上,△ABC的重心与此抛物线的焦点F重合(如图)。(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标。

(1)抛物线方程为y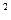 =32x,焦点F的坐标为(8,0)。
=32x,焦点F的坐标为(8,0)。
(2)点M的坐标为(11,-4)。
 =32x,焦点F的坐标为(8,0)。
=32x,焦点F的坐标为(8,0)。(2)点M的坐标为(11,-4)。
(1)由点A(2,8)在抛物线y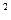 =2px上,有8
=2px上,有8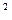 =2p·2,解得p=16。
=2p·2,解得p=16。
所以抛物线方程为y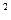 =32x,焦点F的坐标为(8,0)。
=32x,焦点F的坐标为(8,0)。
(2)如原题上图,由于F(8,0)是△ABC的重心,M是BC的中点,所以F是线段AM的定比分点,且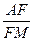 =2。设点M的坐标为(x
=2。设点M的坐标为(x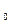 ,y
,y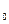 ),则
),则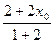 =8,
=8,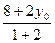 =0,
=0,
解得x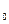 =11,y
=11,y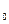 =-4。所以点M的坐标为(11,-4)。
=-4。所以点M的坐标为(11,-4)。
 =2px上,有8
=2px上,有8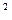 =2p·2,解得p=16。
=2p·2,解得p=16。所以抛物线方程为y
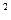 =32x,焦点F的坐标为(8,0)。
=32x,焦点F的坐标为(8,0)。(2)如原题上图,由于F(8,0)是△ABC的重心,M是BC的中点,所以F是线段AM的定比分点,且
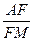 =2。设点M的坐标为(x
=2。设点M的坐标为(x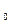 ,y
,y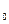 ),则
),则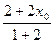 =8,
=8,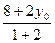 =0,
=0,解得x
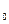 =11,y
=11,y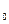 =-4。所以点M的坐标为(11,-4)。
=-4。所以点M的坐标为(11,-4)。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
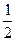 ,1)
,1)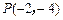 的抛物线的标准方程.
的抛物线的标准方程.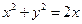 及抛物线S:
及抛物线S: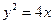 ,过圆心
,过圆心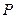 作直线
作直线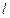 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为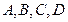 ,如果线段
,如果线段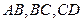 的长按此顺序构成一个等差数列,求直线l的方程.
的长按此顺序构成一个等差数列,求直线l的方程.