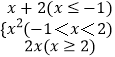题目内容

【题目】等差数列{an}的前n项和为Sn ， 已知a1=10，a2为整数，且Sn≤S4 ， 设 ，则数列{bn}的前项和Tn为（ ）
A.
B.
C.
D.

【答案】B
【解析】解：设等差数列{an}的公差为d，∵等差数列{an}的前项和为Sn ， 且Sn≤S4 ， ∴S4为其前项和中的最大值，
∴ ，
又a1=10，
∴ ，解得：﹣ ≤d＜﹣ ，又a2为整数，
∴公差d=a2﹣a1为整数，
∴d=﹣3．
∴an=10+（n﹣1）×（﹣3）=13﹣3n．
又 = = （ ﹣ ），
∴Tn=b1+b2+…+bn= （ ﹣ + ﹣ +…+ ﹣ ）= （ ﹣ ）= ．
故选：B．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系．

练习册系列答案
相关题目

【题目】设f（x）= ，
（1）在下列直角坐标系中画出f（x）的图象；

（2）若f（x）=3，求x的值；
（3）看图象写出函数f（x）的值域．

【题目】设函数f（x）=aex﹣x﹣1，a∈R．
（Ⅰ）当a=1时，求f（x）的单调区间；
（Ⅱ）当x∈（0，+∞）时，f（x）＞0恒成立，求a的取值范围；
（Ⅲ）求证：当x∈（0，+∞）时，ln ＞ ．

【题目】已知点，点是圆上的任意一点，设为该圆的圆心，并且线段的垂直平分线与直线交于点.

（1）求点的轨迹方程；

（2）已知两点的坐标分别为， ，点是直线上的一个动点，且直线分别交（1）中点的轨迹于两点（四点互不相同），证明：直线恒过一定点，并求出该定点坐标.

【题目】已知分别是椭圆 的长轴与短轴的一个端点， 分别是椭圆的左、右焦点， 椭圆上的一点， 的周长为.

（1）求椭圆的方程；

（2）若是圆上任一点，过点作椭圆的切线，切点分别为，求证： .

【题目】直角坐标系中，曲线与轴负半轴交于点，直线与相切于， 为上任意一点， 为在上的射影， 为的中点．

（Ⅰ）求动点的轨迹的方程；

（Ⅱ）轨迹与轴交于，点为曲线上的点，且， ，试探究三角形的面积是否为定值，若为定值，求出该值；若非定值，求其取值范围．

【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且 ， ．
（Ⅰ）求sinB的值；
（Ⅱ）若 ，求△ABC的面积．

【题目】将函数y=sin2x的图象向左平移 个单位，再向上平移1个单位，所得图象的函数解析式是（ ）
A.y=cos2x
B.y=2cos2x
C.
D.y=2sin2x?

【题目】已知两点A（﹣2，0），B（0，2），点C是圆x2+y2﹣2x=0上的任意一点，则△ABC的面积最小值是 ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网