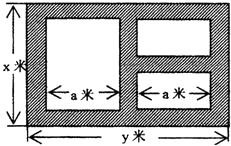
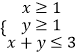题目内容
【题目】直角坐标系![]() 中,曲线
中,曲线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,直线
,直线![]() 与
与![]() 相切于
相切于![]() ,
, ![]() 为
为![]() 上任意一点,
上任意一点, ![]() 为
为![]() 在
在![]() 上的射影,
上的射影, ![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)轨迹![]() 与
与![]() 轴交于
轴交于![]() ,点
,点![]() 为曲线
为曲线![]() 上的点,且
上的点,且![]() ,
, ![]() ,试探究三角形
,试探究三角形![]() 的面积是否为定值,若为定值,求出该值;若非定值,求其取值范围.
的面积是否为定值,若为定值,求出该值;若非定值,求其取值范围.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)依题意,可知![]() ,
, ![]() .……………2分
.……………2分
因为![]() 为
为![]() 上动点,代入整理,即可得到点
上动点,代入整理,即可得到点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)由![]() 求
求![]() ,同理
,同理![]() ,得
,得![]() ,再
,再
求则![]() 到
到![]() 的距离
的距离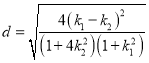 .即可表示
.即可表示![]() 的面积.
的面积.
试题解析:(Ⅰ)依题意,可知![]() ,直线
,直线![]() .
.
设![]() ,依题意,可知
,依题意,可知![]() ,
, ![]() .
.
因为![]() 为
为![]() 上动点,所以
上动点,所以![]() ,
,
可得动点![]() 的轨迹
的轨迹![]() 的方程
的方程![]() .
.
(Ⅱ)依题意,不妨记![]() ,
, ![]() ,设
,设![]() 的斜率为
的斜率为![]() ,因为
,因为![]() ,所以
,所以![]() 的斜率也为
的斜率也为![]() ;同理,设
;同理,设![]() 的斜率为
的斜率为![]() ,因为
,因为![]() ,所以
,所以![]() 的斜率也为
的斜率也为![]() .
.
设![]() ,由
,由![]() 得
得![]() ,则
,则![]() ①;
①;
同理,由![]() 得
得![]() ,则
,则![]() ②.
②.
联立①②,消去![]() 可得
可得![]() ,不妨设
,不妨设![]() ,
, ![]() .
.
由![]() 可得
可得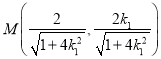 ,则
,则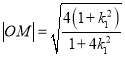 .
.
由![]() 可得
可得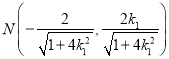 .
.
则![]() 到
到![]() 的距离
的距离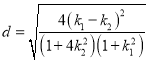 .
.
则三角形![]() 的面积
的面积![]()
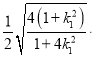
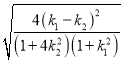
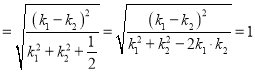 .
.

【题目】为提高市场销售业绩,某公司设计两套产品促销方案(方案1运作费用为![]() 元/件;方案2的的运作费用为
元/件;方案2的的运作费用为![]() 元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
(Ⅰ)请根据列联表提供的信息,为该公司今年选择一套较为有利的促销方案(不必说明理由);
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的![]() 组售价
组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)(
(单位:件)(![]() )如下表所示:
)如下表所示:
售价 |
|
|
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
|
|
(ⅰ)请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
(ⅱ)根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
|
|
|
|
|
| ||
参考公式:相关指数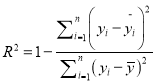 .
.