题目内容
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且 ![]() ,
, ![]() .
.
(Ⅰ)求sinB的值;
(Ⅱ)若 ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】解:(Ⅰ)因为 ![]() ,
, ![]() ,
,
所以 ![]() .
.
由已知得 ![]() .
.
所以 ![]() =
= ![]() .
.
(Ⅱ)由(Ⅰ)知C= ![]() ,所以sinC=
,所以sinC= ![]() 且
且 ![]() .
.
由正弦定理得 ![]() .
.
又因为 ![]() ,
,
所以c=5, ![]() .
.
所以 ![]()
【解析】(Ⅰ)先根据 ![]() 求得cosA的值,再由
求得cosA的值,再由 ![]() 得到
得到 ![]() ,然后根据两角和与差的公式可求得sinB的值.(Ⅱ)由C=
,然后根据两角和与差的公式可求得sinB的值.(Ⅱ)由C= ![]() 可求得sinC的值,进而根据正弦定理可求得a,c的关系,再由
可求得sinC的值,进而根据正弦定理可求得a,c的关系,再由 ![]() 可求出a,c的值,最后根据三角形的面积公式可求得答案.
可求出a,c的值,最后根据三角形的面积公式可求得答案.
【考点精析】本题主要考查了同角三角函数基本关系的运用和正弦定理的定义的相关知识点,需要掌握同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() ;正弦定理:
;正弦定理:![]() 才能正确解答此题.
才能正确解答此题.

【题目】为提高市场销售业绩,某公司设计两套产品促销方案(方案1运作费用为![]() 元/件;方案2的的运作费用为
元/件;方案2的的运作费用为![]() 元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
(Ⅰ)请根据列联表提供的信息,为该公司今年选择一套较为有利的促销方案(不必说明理由);
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的![]() 组售价
组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)(
(单位:件)(![]() )如下表所示:
)如下表所示:
售价 |
|
|
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
|
|
(ⅰ)请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
(ⅱ)根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
|
|
|
|
|
| ||
参考公式:相关指数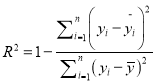 .
.

