Question

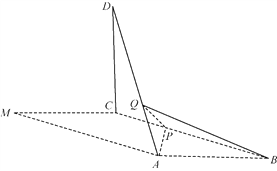
【题目】已知平面四边形MNPQ中，MN＝，MP＝1，MP⊥MN，PQ⊥QM．

（Ⅰ）若PQ＝，求NQ的值；

（Ⅱ）若∠MQN＝30°，求sin∠QMP的值．

Answer 1

【答案】（Ⅰ）（Ⅱ）.

【解析】

（Ⅰ）由题意可得∠QMN＝150，根据余弦定即可求出，

（Ⅱ）∠QMP＝θ，由题意可得QM，∠MNQ，在△MNQ中，由正弦定理结合三角恒等变换整理可得tanθ，再根据同角三角函数的基本关系，即可求出

解：（Ⅰ）如图：∵MN＝，MP＝1，MP⊥MN，PQ⊥QM，

∴PQ＝＝，

∴sin∠QMP＝＝，

∴∠QMP＝60°，

∴QM＝PM＝，

∴∠QMN＝150°，

由余弦定理可得NQ2＝QM2+MN2﹣2MNQMcos∠QMN＝+3﹣2×××（﹣）＝，

∴NQ＝，

（2）：∵MN＝，MP＝1，MP⊥MN，PQ⊥QM

设∠QMP＝θ，由题意可得QM＝cosθ，∠MNQ＝60°﹣θ，

在△MNQ中，由正弦定理可得＝，

即＝2，

整理可得tanθ＝，

∵sin2θ+cos2θ＝1，

θ＝，

故sin∠QMP＝．