题目内容
【题目】已知函数f(x)=mx3+x﹣sinx(m∈R).
(1)当m=0时,(i)求y=f(x)在(![]() ,f(
,f(![]() ))处的切线方程;
))处的切线方程;
(ii)证明:f(x)<ex;
(2)当x≥0时,函数f(x)单调递减,求m的取值范围.
【答案】(1)(i)![]() (ii)见解析(2)
(ii)见解析(2)![]()
【解析】
(1)(i) 根据导数的几何意义求出切线斜率,由点斜式即可得结果;(ii ) 当![]() 时,原命题等价于
时,原命题等价于![]() ,结合
,结合![]() ,即证
,即证![]() ,令
,令![]() ,利用异数研究其单调性,可得
,利用异数研究其单调性,可得![]() ,从而可得结论;(2)依题意
,从而可得结论;(2)依题意![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,求导
,求导![]() ,令
,令![]() ,利用导数研究其单调性可,通过对
,利用导数研究其单调性可,通过对![]() 分类讨论,即可筛选出符合题意的
分类讨论,即可筛选出符合题意的![]() 取值范围.
取值范围.
(1)当![]() 时,
时,![]() .
.
(i)![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(ii)原命题等价于![]() ,
,
![]() ,即证
,即证![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减,
单调递减,
![]() ,
,
![]() ,取等号条件不一致,
,取等号条件不一致,
![]() ,
,
![]() .
.
(2)依题意,![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
(i)当![]() 时,
时,![]() 单调递减,
单调递减,
![]() ,即
,即![]() ,符合题意.
,符合题意.
(ii)当![]() 时,
时,![]() ,不符合题意,舍去.
,不符合题意,舍去.
(iii)当![]() 时,令
时,令![]() ,则
,则![]() ,
,
由![]() ,
,
![]() ,
,
![]() ,使
,使![]() ,
,
所以当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
所以当![]() 时,
时,![]() ,即
,即![]() ,
,
所以当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,即
,即![]() ,不符合题意,舍去,
,不符合题意,舍去,
故![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值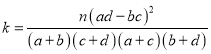
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
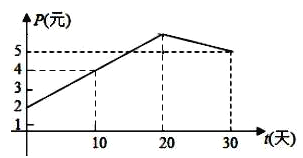
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对![]() ,点
,点![]() 落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
第t天 | 6 | 13 | 20 | 27 |
M(万股) | 34 | 27 | 20 | 13 |
(1)根据提供的图象,写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式![]() ______;
______;
(2)根据表中数据,写出日交易量M(万股)与时间t(天)的一次函数关系式:![]() ______;
______;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
