题目内容
【题目】已知![]() ,若过
,若过![]() 轴上的一点
轴上的一点![]() 可以作一直线与
可以作一直线与![]() 相交于
相交于![]() ,
,![]() 两点,且满足
两点,且满足![]() ,则
,则![]() 的取值范围为_______.
的取值范围为_______.
【答案】![]()
【解析】
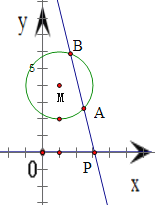
由圆的方程,可得M(1,4)且半径为2,由PA=BA,利用圆的几何性质得动点P到圆M的最近的点的距离小于或等于4,由此建立关于a的不等式,解得即可.
∵圆M:(x﹣1)2+(y﹣4)2=4,∴圆心为M(1,4),半径r=2,直径为4,故弦长BA的范围是(0,4].又∵PA=BA,∴动点P到圆M的最近的点的距离小于或等于4,
∵圆与x轴相离,可得P到圆上的点的距离恒大于0.
∴P到M的距离小于或等于6,根据两点间的距离公式有:![]() ,
,
解之得1﹣2![]() ≤a≤1+2
≤a≤1+2![]() ,即a的取值范围为[1﹣2
,即a的取值范围为[1﹣2![]() ,1+2
,1+2![]() ]
]
故答案为:[1﹣2![]() ,1+2
,1+2![]() ]
]

【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对![]() ,点
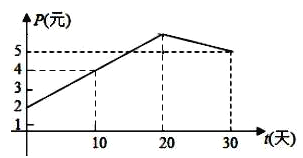
,点![]() 落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
第t天 | 6 | 13 | 20 | 27 |
M(万股) | 34 | 27 | 20 | 13 |
(1)根据提供的图象,写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式![]() ______;
______;
(2)根据表中数据,写出日交易量M(万股)与时间t(天)的一次函数关系式:![]() ______;
______;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 | 非优秀 | 总计 |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;(把列联表自己画到答题卡上)
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |