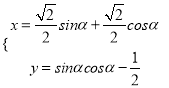题目内容
【题目】在底面是菱形的四棱锥![]() 中,
中,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上.
上.
①如图1,若点![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
②如图2,若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
【答案】(1)证明见解析;(2)①证明见解析;②存在,证明见解析
【解析】
(1)首先根据题意得到![]() 是等边三角形,根据勾股定理得到
是等边三角形,根据勾股定理得到![]() ,
,![]() ,再根据线面垂直的判定即可证明
,再根据线面垂直的判定即可证明![]() 平面
平面![]() .
.
(2)①根据三角形中位线即可得到![]() ,再根据线面平行的判定即可证明
,再根据线面平行的判定即可证明![]() 平面
平面![]() .②存在
.②存在![]() 是
是![]() 中点,使得
中点,使得![]() 平面
平面![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() .根据三角形中位线即可得到
.根据三角形中位线即可得到![]() 面
面![]() ,
,![]() 面
面![]() ,即平面
,即平面![]() 平面
平面![]() ,再利用面面平行的性质即可得到
,再利用面面平行的性质即可得到![]() 平面
平面![]() .
.
(1)在菱形![]() 中,
中,![]()
![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
又![]() ,故菱形边长为
,故菱形边长为![]() ,
,
在![]() 中,
中,![]() ,则
,则![]()
同理![]() .
.
又![]() 面
面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
(2)①连结![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
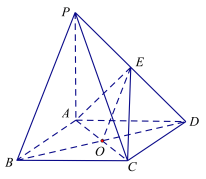
在菱形![]() 中
中![]() 为
为![]() 中点又
中点又![]() 是线段
是线段![]() 的中点,
的中点,
所以![]() .
.
∵![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.
②存在,![]() 是
是![]() 中点.
中点.
取![]() 中点
中点![]() ,连结
,连结![]() .
.
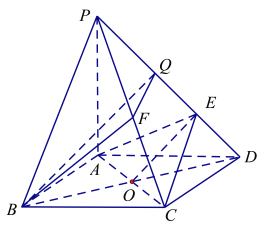
在![]() 中
中![]() ,
,![]() 为
为![]() 中点,则
中点,则![]() ,
,
又∵![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
同理![]() 面
面![]() .
.
又∵![]() 面
面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 面
面![]() ∴
∴![]() 平面
平面![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 | 非优秀 | 总计 |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;(把列联表自己画到答题卡上)
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |