题目内容
用反证法证明“ ,
, 可被5整除,那么
可被5整除,那么 中至少有一个能被5整除”,则假设内容是_____________________________________________________.
中至少有一个能被5整除”,则假设内容是_____________________________________________________.
 ,
, 可被5整除,那么
可被5整除,那么 中至少有一个能被5整除”,则假设内容是_____________________________________________________.
中至少有一个能被5整除”,则假设内容是_____________________________________________________.“ 都不能被5整除”
都不能被5整除”
 都不能被5整除”
都不能被5整除”试题分析:反证法是从结论的反面出发,经过推理得出与已知或者公理、定理矛盾的结论,从而说明原命题成立的证明方法,应假设“
 都不能被5整除”.
都不能被5整除”.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是一个自然数,
是一个自然数, 是
是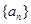 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; 时,求证:存在
时,求证:存在 ,使得
,使得 .
. an+n-4,λ∈R,n∈N+,对任意λ
an+n-4,λ∈R,n∈N+,对任意λ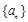 的通项公式
的通项公式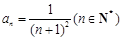 ,记
,记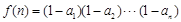 .
.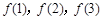 的值;
的值;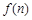 ,并证明.
,并证明. >
> ”时,假设的内容应为______________.
”时,假设的内容应为______________. 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( ) ,且
,且 求证:
求证: 中至少有一个是负数。
中至少有一个是负数。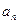 }的前n项和为
}的前n项和为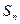 ,并且满足
,并且满足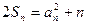 ,
,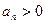 (n∈N*).
(n∈N*).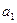 ,
,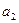 ,
,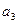 ;
;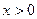 ,
,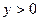 ,且
,且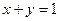 ,证明:
,证明: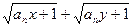 ≤
≤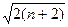 .
.