题目内容
(本小题15分)
设数列{
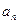 }的前n项和为
}的前n项和为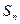 ,并且满足
,并且满足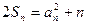 ,
,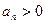 (n∈N*).
(n∈N*).(Ⅰ)求
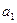 ,
,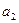 ,
,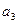 ;
;(Ⅱ)猜想{
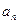 }的通项公式,并用数学归纳法加以证明;
}的通项公式,并用数学归纳法加以证明;(Ⅲ)设
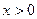 ,
,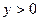 ,且
,且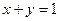 ,证明:
,证明: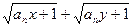 ≤
≤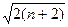 .
.解:(Ⅰ)分别令 ,2,3,得
,2,3,得

∵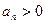 ,∴
,∴ ,
, ,
, .
.
(Ⅱ)证法一:猜想: ,由
,由 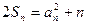 ①
①
可知, 当
当 ≥2时,
≥2时, ②
②
①-②,得 ,即
,即 .
.
1)当 时,
时, ,∵
,∵ ,∴
,∴ ;
;
2)假设当 (
( ≥2)时,
≥2)时, .
.
那么当 时,
时,


 ,
,
∵ ,
, ≥2,∴
≥2,∴ ,
,
∴ .
.
这就是说,当 时也成立,
时也成立,
 ∴
∴ (
( ≥2). 显然
≥2). 显然 时,也适合.
时,也适合.
故对于n∈N*,均有
(Ⅲ)要证 ≤
≤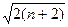 ,
,
只要证 ≤
≤ ,
,
即
 ≤
≤ ,
,
将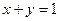 代入,得
代入,得 ≤
≤ ,.m
,.m
即要证 ≤
≤
 ,即
,即 ≤1.
≤1.
∵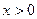 ,
,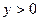 ,且
,且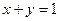 ,∴
,∴ ≤
≤ ,
,
即 ≤
≤ ,故
,故 ≤1成立,所以原不等式成立.
≤1成立,所以原不等式成立.
 ,2,3,得
,2,3,得
∵
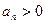 ,∴
,∴ ,
, ,
, .
.(Ⅱ)证法一:猜想:
 ,由
,由 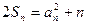 ①
①可知,
 当
当 ≥2时,
≥2时, ②
②①-②,得
 ,即
,即 .
.1)当
 时,
时, ,∵
,∵ ,∴
,∴ ;
;2)假设当
 (
( ≥2)时,
≥2)时, .
.那么当
 时,
时,

 ,
,∵
 ,
, ≥2,∴
≥2,∴ ,
,∴
 .
.这就是说,当
 时也成立,
时也成立, ∴
∴ (
( ≥2). 显然
≥2). 显然 时,也适合.
时,也适合.故对于n∈N*,均有

(Ⅲ)要证
 ≤
≤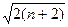 ,
,只要证
 ≤
≤ ,
,即

 ≤
≤ ,
,将
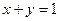 代入,得
代入,得 ≤
≤ ,.m
,.m即要证
 ≤
≤
 ,即
,即 ≤1.
≤1.∵
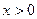 ,
,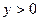 ,且
,且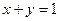 ,∴
,∴ ≤
≤ ,
,即
 ≤
≤ ,故
,故 ≤1成立,所以原不等式成立.
≤1成立,所以原不等式成立.略

练习册系列答案
相关题目
 中,若
中,若 ,则
,则 ,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想 ,
, 可被5整除,那么
可被5整除,那么 中至少有一个能被5整除”,则假设内容是_____________________________________________________.
中至少有一个能被5整除”,则假设内容是_____________________________________________________. ,那么
,那么 ”时,假设的内容应是
”时,假设的内容应是

 若
若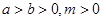 ,则
,则 与
与 的关系( )
的关系( ) ,如果
,如果 可被5整除,那么
可被5整除,那么 ,
, 至少有1个能被5整除.”则假设的内容是 ( )
至少有1个能被5整除.”则假设的内容是 ( ) ,求证:
,求证: ,用反证法证明时,可假设
,用反证法证明时,可假设 ;
; ,
, ,求证:方程
,求证:方程 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设 ,以下结论正确的是( )
,以下结论正确的是( ) 与
与 的假设都错误
的假设都错误 …
… >
> (n∈N*,且n>2)时,第二步由
(n∈N*,且n>2)时,第二步由
 +
+ -
- 
 +
+
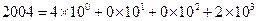 ,那么在5进制中数码2004折合成十进制为
,那么在5进制中数码2004折合成十进制为