题目内容
已知数列{an}满足a1=λ,an+1= an+n-4,λ∈R,n∈N+,对任意λ
an+n-4,λ∈R,n∈N+,对任意λ
∈R,证明:数列{an}不是等比数列.
 an+n-4,λ∈R,n∈N+,对任意λ
an+n-4,λ∈R,n∈N+,对任意λ∈R,证明:数列{an}不是等比数列.
见解析
假设存在一个实数λ,使{an}为等比数列,则有 =a1a3,即
=a1a3,即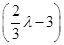 2=λ
2=λ ,即:
,即: λ2-4λ+9=
λ2-4λ+9= λ2-4λ,∴9=0,矛盾.
λ2-4λ,∴9=0,矛盾.
所以,数列{an}不是等比数列.
 =a1a3,即
=a1a3,即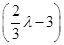 2=λ
2=λ ,即:
,即: λ2-4λ+9=
λ2-4λ+9= λ2-4λ,∴9=0,矛盾.
λ2-4λ,∴9=0,矛盾.所以,数列{an}不是等比数列.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
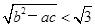 a.
a.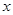
 ,那么
,那么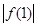 ,
,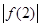 ,
,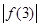 中至少有一个不小于
中至少有一个不小于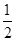 ”时,反设正确的是( )
”时,反设正确的是( ) =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.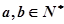 ,
,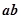 可被5整除,那么
可被5整除,那么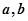 中至少有一个能被5整除”,则假设内容是_____________________________________________________.
中至少有一个能被5整除”,则假设内容是_____________________________________________________.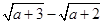 <
<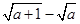 ,其中a≥0.=
,其中a≥0.= 若
若 ,则
,则 与
与 的关系( )
的关系( )