题目内容
设 是一个自然数,
是一个自然数, 是
是 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列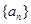 :
: 是自然数,
是自然数, (
( ,
, ).
).
(1)求 ,
, ;
;
(2)若 ,求证:
,求证: ;
;
(3)当 时,求证:存在
时,求证:存在 ,使得
,使得 .
.
 是一个自然数,
是一个自然数, 是
是 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列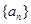 :
: 是自然数,
是自然数, (
( ,
, ).
).(1)求
 ,
, ;
;(2)若
 ,求证:
,求证: ;
;(3)当
 时,求证:存在
时,求证:存在 ,使得
,使得 .
.(1) ,
, ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.
 ,
, ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.试题分析:本题是一道新定义题,主要考查归纳推理、数学归纳法、分类讨论思想等基础知识,考查学生的分析问题解决问题的能力和转化能力.第一问,由于
 是a的各位数字的平方和,所以
是a的各位数字的平方和,所以 ,
, ;第二问,通过题干中给出的
;第二问,通过题干中给出的 的定义设出
的定义设出 的值,利用
的值,利用 ,得到
,得到 的值,然后用作差法比较
的值,然后用作差法比较 和
和 的大小;第三问,由已知条件
的大小;第三问,由已知条件
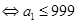 ,由于
,由于 且
且 ,得
,得 ,由归纳推理得
,由归纳推理得 ,再用数学归纳法证明一下,因此存在
,再用数学归纳法证明一下,因此存在 (
( ),有
),有 ,再分类讨论p、q的情况,得出结论.
,再分类讨论p、q的情况,得出结论.(1)
 ;
; . 5分
. 5分(2)假设
 是一个
是一个 位数(
位数( ),
),那么可以设
 ,
,其中
 且
且 (
( ),且
),且 .
.由
 可得,
可得, .
. 所以
所以 .
.因为
 ,所以
,所以 .
.而
 ,
,所以
 ,即
,即 . 9分
. 9分(3)由
 ,即
,即 ,可知
,可知 .
.同理
 ,可知
,可知 .
.由数学归纳法知,对任意
 ,有
,有 .
.即对任意
 ,有
,有 .
.因此,存在
 (
( ),有
),有 .
.则
 ,
, , ,
, , ,
,可得对任意
 ,
, ,有
,有 .
.设
 ,即对任意
,即对任意 ,有
,有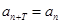 .
.若
 ,取
,取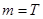 ,
, ,则有
,则有 .
.若
 ,由
,由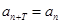 ,可得
,可得 ,
,取
 ,
, ,则有
,则有 . 14分
. 14分
练习册系列答案
相关题目
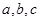 为三角形
为三角形 的三边,求证:
的三边,求证:
 a.
a.
 ,那么
,那么 ,
, ,
, 中至少有一个不小于
中至少有一个不小于 ”时,反设正确的是( )
”时,反设正确的是( ) +
+ 是无理数”时,假设正确的是( )
是无理数”时,假设正确的是( ) 是有理数
是有理数 或
或 ,
, 可被5整除,那么
可被5整除,那么 中至少有一个能被5整除”,则假设内容是_____________________________________________________.
中至少有一个能被5整除”,则假设内容是_____________________________________________________. ,求证:
,求证: ,用反证法证明时,可假设
,用反证法证明时,可假设 ;
; ,
, ,求证:方程
,求证:方程 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设 ,以下结论正确的是( )
,以下结论正确的是( ) 与
与 的假设都错误
的假设都错误