题目内容
【题目】已知集合M={1，2，3}，N={1，2，3，4}，定义函数f：M→N．若点A（1，f（1））、B（2，f（2））、C（3，f（3）），△ABC的外接圆圆心为D，且 
，则满足条件的函数f（x）有（ ）
A.6个
B.10个
C.12个
D.16个
【答案】C
【解析】解：由 
，说明△ABC是等腰三角形，且BA=BC，必有f（1）=f（3），f（1）≠f（2）；
点A（1，f（1））、当f（1）=1=f（3）时f（2）=2、3、4，三种情况．
f（1）=f（3）=2；f（2）=1、3、4，有三种．
f（1）=f（3）=3；f（2）=2、1、4，有三种．
f（1）=f（3）=4；f（2）=2、3、1，有三种．
因而满足条件的函数f（x）有12种．
故选C
【考点精析】根据题目的已知条件，利用向量的共线定理和分类加法计数原理的相关知识可以得到问题的答案，需要掌握设
，
，其中
，则当且仅当
时，向量
、
共线；做一件事情，完成它有N类办法，在第一类办法中有M1种不同的方法，在第二类办法中有M2种不同的方法，……，在第N类办法中有MN种不同的方法，那么完成这件事情共有M1+M2+……+MN种不同的方法．
【题目】某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关．现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组：[50，60），[60，70），[70，80），[80，90），[90，100）分别加以统计，得到如图所示的频率分布直方图．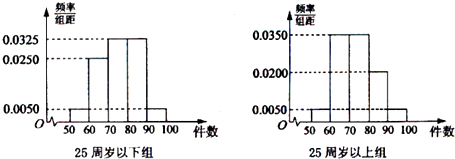
附表：
P（K2≥k） | 0.100 | 0.010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
K2= 
，（其中n=a+b+c+d）
（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的频率．
（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2的列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？
生产能手 | 非生产能手 | 合计 | |
25周岁以上组 | |||
25周岁以下组 | |||
合计 |
