Question

【题目】如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1 ， D1C1上，A1E=D1F=4．过E，F的平面α与此长方体的面相交，交线围成一个正方形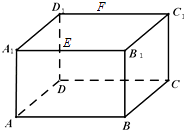

（1）在图中画出这个正方形（不必说出画法和理由）
（2）求平面α把该长方体分成的两部分体积的比值．

Answer 1

【答案】
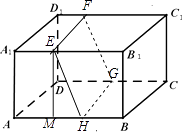
（1）解：交线围成的正方形EFGH如图所示；
（2）解：作EM⊥AB，垂足为M，则AM=A1E=4，EB1=12，EM=AA1=8．

因为EFGH为正方形，所以EH=EF=BC=10，

于是MH= =6，AH=10，HB=6．

因为长方体被平面α分成两个高为10的直棱柱，

所以其体积的比值为 ．

【解析】（1）利用平面与平面平行的性质，可在图中画出这个正方形；（2）求出MH= =6，AH=10，HB=6，即可求平面a把该长方体分成的两部分体积的比值．
【考点精析】解答此题的关键在于理解平面的基本性质及推论的相关知识，掌握如果一条直线上的两点在一个平面内，那么这条直线在此平面内;过不在一条直线上的三点，有且只有一个平面;如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．