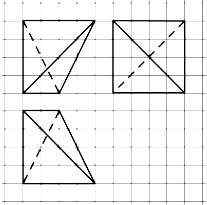题目内容
【题目】如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(﹣2,0),C(a,0),(a>0),设△AOB和△COD的
外接圆圆心分别为点M、N.
(Ⅰ)若⊙M与直线CD相切,求直线CD的方程;
(Ⅱ)若直线AB截⊙N所得弦长为4,求⊙N的标准方程.
【答案】解(Ⅰ)圆心M(﹣1,1),∴圆M方程为(x+1)2+(y﹣1)2=2,直线 lCD方程为x+y﹣a=0
∵⊙M与直线lCD相切,∴圆心 M到直线lCD的距离 ![]() ,
,
∴|a|=2,又a>0,a=2
∴直线lCD的方程为x+y﹣2=0;
(Ⅱ)直线lAB方程为:x﹣y+2=0,圆心 ![]() ,
,
∴圆心N到直线lAB距离为 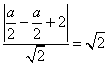 ,
,
∵直线lAB截⊙N的所得弦长为4
∴ ![]() ,∴a2=12,又a>0,
,∴a2=12,又a>0, ![]()
∴⊙N的标准方程为 ![]()
【解析】先根据条件求圆的标准方程,再,利用直线与圆相切时,点线距离等于半径长求解;(2)利用圆心N到直线lAB距离及直线lAB截⊙N的所得弦长为4,可求圆的标准方程.
【考点精析】掌握一般式方程和圆的标准方程是解答本题的根本,需要知道直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0);圆的标准方程:
(A,B不同时为0);圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.

练习册系列答案
相关题目