题目内容
【题目】在某亲子游戏结束时有一项抽奖活动,抽奖规则是:盒子里面共有4个小球,小球上分别写有0,1,2,3的数字,小球除数字外其他完全相同,每对亲子中,家长先从盒子中取出一个小球,记下数字后将小球放回,孩子再从盒子中取出一个小球,记下小球上数字将小球放回.抽奖活动的奖励规则是:①若取出的两个小球上数字之积大于4,则奖励飞机玩具一个;②若取出的两个小球上数字之积在区间上![]() ,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
(1)求每对亲子获得飞机玩具的概率;
(2)试比较每对亲子获得汽车玩具与获得饮料的概率,哪个更大?请说明理由.
【答案】(1)![]() ;(2)获得饮料的概率更大.
;(2)获得饮料的概率更大.
【解析】
(1)利用列举法求出基本事件总数有16个,记“获得飞机玩具”为事件![]() ,则事件
,则事件![]() 包含的基本事件有3个,由此能求出每对亲子获得飞机玩具的概率.
包含的基本事件有3个,由此能求出每对亲子获得飞机玩具的概率.
(2)记“获得汽车玩具”为事件![]() ,“获得饮料”为事件
,“获得饮料”为事件![]() ,利用列举法求出事件
,利用列举法求出事件![]() 包含的基本事件有6个,由此能求出每对亲子获得汽车玩具的概率
包含的基本事件有6个,由此能求出每对亲子获得汽车玩具的概率![]() ,再由对立事件概率计算公式得每对亲子获得饮料的概率
,再由对立事件概率计算公式得每对亲子获得饮料的概率![]() ,由此能求出每对亲子获得汽车玩具小于获得饮料的概率.
,由此能求出每对亲子获得汽车玩具小于获得饮料的概率.
解:(1)基本事件总数有16个,分别为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
记“获得飞机玩具”为事件![]() ,则事件
,则事件![]() 包含的基本事件有3个,分别为:
包含的基本事件有3个,分别为:![]() ,
,![]() ,
,![]() ,
,
∴每对亲子获得飞机玩具的概率![]() .
.
(2)记“获得汽车玩具”为事件![]() ,“获得饮料”为事件
,“获得饮料”为事件![]() ,
,
事件![]() 包含的基本事件有6个,分别为:
包含的基本事件有6个,分别为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴每对亲子获得汽车玩具的概率![]() ,
,
每对亲子获得饮料的概率![]() ,
,
∴每对亲子获得汽车玩具小于获得饮料的概率.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】随着我国中医学的发展,药用昆虫的使用相应愈来愈多.每年春暖以后至寒冬前,是昆虫大量活动与繁殖季节,易于采集各种药用昆虫.已知一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
温度 | 10 | 11 | 13 | 12 | 8 |
产卵数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记这两天药用昆虫的产卵分别为![]() ,
,![]() ,求事件“
,求事件“![]() ,
,![]() 均不小于25”的概率;
均不小于25”的概率;
(2)科研人员确定的研究方案是:先从这五组数据中任选2组,用剩下的3组数据建立![]() 关于
关于![]() 的线性回归方程,再对被选取的2组数据进行检验.
的线性回归方程,再对被选取的2组数据进行检验.
(ⅰ)若选取的是3月2日与30日的两组数据,请根据3月7日、15日和22日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(ⅱ)若由线性回归方程得到的估计数据与选出的检验数据的误差均不超过2个,则认为得到的线性回归方程是可靠的,试问(ⅰ)中所得的线性回归方程是否可靠?
附:回归直线的斜率和截距的最小二乘估计公式分别为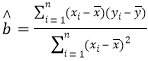 ,
,![]() .
.
【题目】某同学用“五点法”画函数![]() 在某一周期内的图象时,列表并填入了部分数据,如下表:
在某一周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
| ① |
| ||
|
|
|
|
|
|
(1)请将上面表格中①的数据填写在答题卡相应位置上,并直接写出函数![]() 的解析式;
的解析式;
(2)若将函数![]() 的图象上所有点的横坐标变为原来的
的图象上所有点的横坐标变为原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象,求当
的图象,求当![]() 时,函数
时,函数![]() 的单调递增区间;
的单调递增区间;
(3)若将函数![]() 图象上的所有点向右平移
图象上的所有点向右平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象. 若
的图象. 若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.