Question

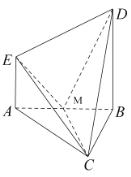
【题目】如图，四边形ABCD为矩形，平面ABCD⊥平面ABE，F为CE的中点，且AE⊥BE．

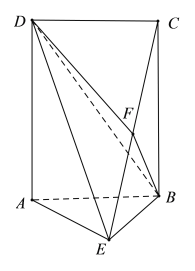
（1）求证：AE∥平面BFD：

（2）求证：BF⊥AE．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

以E为原点，EB为x轴，EA为y轴，过E作平面ABE的垂线为z轴，建立空间直角坐标系，（1）设出的长表示出各点坐标，由直线的方向向量与平面的法向量垂直得证线面平行；

（2）直接由方向向量垂直得两直线垂直．

（1）以E为原点，EB为x轴，EA为y轴，过E作平面ABE的垂线为z轴，建立空间直角坐标系，

由于平面平面，，是这两个平面的交线，都在平面上，所以平面，平面，所以轴，轴，

设BE＝a，AE＝b，AD＝c，则A（0，b，0），E（0，0，0），F（），B（a，0，0），D（0，b，c），

（0，﹣b，0），（，0，），（﹣a，b，c），设平面BDF的法向量（x，y，z），

则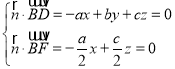，取x＝c，得（c，0，a），∵AE平面BDE，0，

∴AE∥平面BFD．

（2）∵（0，﹣b，0），（，0，），∴0，∴BF⊥AE．