题目内容
【题目】从5名男生和4名女生中选出4人去参加座谈会,问:
(1)如果4人中男生和女生各选2人,有多少种选法?
(2)如果男生中的甲与女生中的乙至少要有1人在内,有多少种选法?
(3)如果4人中必须既有男生又有女生,有多少种选法?
【答案】(1)30;(2)91种;(3)120种.
【解析】试题分析:(1)根据题意,分别计算“从5名男生中选出2人”和“从4名女生中选出2人”的选法数目,由分步计数原理计算可得答案;
(2)用间接法分析:先计算在9人中任选4人的选法数目,再排除其中“甲乙都没有入选”的选法数目,即可得答案;
(3)用间接法分析:先计算在9人中任选4人的选法数目,再排除其中“只有男生”和“只有女生”的选法数目,即可得答案.
试题解析:
(1) ![]() ;
;
(2)方法1:(间接法)
在9人选4人的选法中,把男甲和女乙都不在内的去掉,就得到符合条件的选法数为:
![]() (种);
(种);
方法2:(直接法)
甲在内乙不在内有![]() 种,乙在内甲不在内有
种,乙在内甲不在内有![]() 种,甲、乙都在内有
种,甲、乙都在内有![]() 种,所以男生中的甲与女生中的乙至少有1人在内的选法共有:
种,所以男生中的甲与女生中的乙至少有1人在内的选法共有:
![]() (种).
(种).
(3)方法1:(间接法)
在9人选4人的选法中,把只有男生和只有女生的情况排除掉,得到选法总数为:
![]() (种);
(种);
方法2:(直接法)
分别按含男1,2,3人分类,得到符合条件的选法总数为:
![]() (种).
(种).

【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
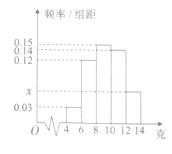
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.